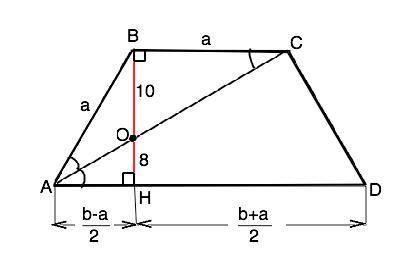
Пусть в трапеции АВСD (BC||AD) диагональ пересекает высоту ВН в точке О, ВО=10 см, ОН=8 см. Примем ВС=AB=CD=а, АD=b.
Диагональ АС и высота ВС при пересечении образуют с частью оснований прямоугольные треугольники, подобные по равным острым углам (при О и накрестлежащим ВСА=СAD). Коэффициент подобия k=ОН:ОВ=8:10=0,8. Поэтому АН=0,8а.
Из ∆ ВАН по т.Пифагора АВ²-АН²=ВН²⇒ а²-0,64а²=0,36а²⇒а=30 см. ⇒ АН=0,8•30=24 см
В равнобедренной трапеции высота из тупого угла делит основание, к которому проведена, на отрезки, меньший из которых равен полуразности оснований, а больший - их полусумме. ⇒
АН=(b-a)/2, HD=(b+a)/2. Из найденного выше (b-a):2=24,⇒ b-30=48 ⇒b=48+30=78.
Площадь трапеции равна произведению высоты на полусумму оснований. Высота ВН=ВО+ОН=18 см, полусумма оснований (a+b):2=(30+78):2=54 см. S(ABCD)=18•54=972 см²
∠AOB = ∪AB = 120°
ΔAOB - образован хордой и двумя радиусами ⇒ равнобедренный
OM - высота, она же биссектриса и медиана ⇒ AM = a/2
∠AOM = ∠BOM = 120°/2 = 60°
ΔAOM - прямоугольный
Длина дуги
Площадь сектора