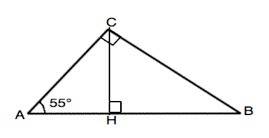
Обозначим треугольник АВС, СН- высота, угол САН=55°
Сумма острых углов прямоугольного треугольника равна 90°. Значит, меньший ∠СВА=90°-55°=35°
Высота делит исходный треугольник на два прямоугольных.
АС - меньший катет. ∠САН=55°, ⇒ ∠АСН=90°-55°=35°
ВС - больший катет. ∠СВН=35°, ⇒ ∠ВСН-90°-35°=55°
Обратим внимание на то, что углы в треугольниках, на которые высота разделила∆ АВС, равны как в них, так и в исходном.
Мы получили одно из важных свойств высоты прямоугольного треугольника.
Высота в прямоугольном треугольнике, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника. Кроме того, каждый из этих треугольников подобен исходному.
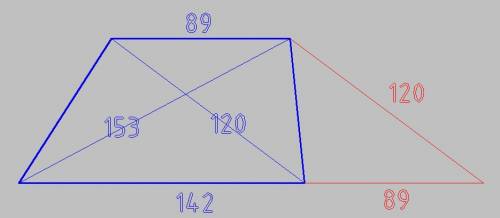
Угол АВС=углу АДС=90 град (как углы, опирающиеся на диаметр АС)
О - центр окружности.
Треугольник АВО = треугольнику АОД - равносторонние, каждая сторона равна радиусу. Значит, все их внутренние углы равны по 60 град.
Тогда, уголВАД=120 град, а угол ВСД= 180-120=60 град.
Дуга АВ = углу АОВ = 60 град
Дуга АД = углу АОД = 60 град
Дуга СД = углу СОД = 180-60=120 град (как смежные)
Дуга ВС = углу ВОС = 180-60=120 град (как смежные)