Question

Нужна с . 1.из точки s проведены перпендикуляр sa и наклонная sb к плоскости "альфа". найти угол между прямой sb и плоскостью "альфа", если sa = √3 см, ab = 1 см 2.точка s равноудалена от сторон правильного треугольника abc. найти расстояние от точки s до плоскости abc, если расстояние от точки s до стороны bc равно √5 см, а сторона треугольника равна 2√3 см 3.отрезок bs перпендикулярен плоскости треугольника abc и имеет длину 2 см. найти расстояние от точки s до стороны ac, если площадь треугольника abc = 12 см², а ac = 6 см.

Answer 1

1.Угол между прямой и плоскостью- это угол между прямой и её проекцией на эту плоскость. АВ - проекция.$tgB= \frac{SA}{AB}= \sqrt{3};$ Угол В равен 60 градусов.
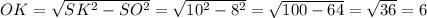
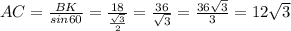
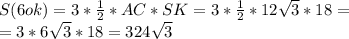
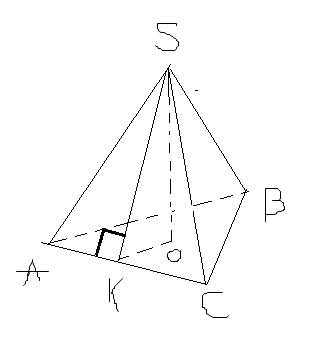
2.SO- перпендикуляр, опущенный на АВС. Т.к.S одинаково удалена от сторон треугольника, то и О тоже, как и любая точка этого перпендикуляра. О - центр вписанной окружности в треугольник АВС.Соединив S с вершинами АВС получим правильную треугольную пирамиду.В грани CSB проведём апофемуSH перпендикулярную СВ. Тогда $AH= \frac{ \sqrt{3} }{2}a$$AH= \frac{ \sqrt{3} }{2} 2 \sqrt{3}=3;$как высота правильного треугольника АВС.$OH= \frac{1}{3}AH=1$  O лежит на пересечении медиан( высот, биссектрис) и делит АН в отношении 2:1, считая от А.Изпрямоугольного треугольникаSOH находим SO:$SO= \sqrt{ SH^{2}- OH^{2} }= \sqrt{5-1}=2. SO=2.$
3.Соединим S с вершинами треугольника АВС. Из точек S и В проведём перпендикуляры к ребру АС. АС будет перпендикулярно SH и BH по теореме о трёх перпендикулярах. Из площади треугольника и основания СА найдём высоту BH:$BH= \frac{2 S_{ABC} }{AC}=4;$Из треугольника SBH по теореме Пифагора найдём SH:$SH= \sqrt{ BH^{2}+ SB^{2} } = \sqrt{16+4}=2 \sqrt{5}.$