Объяснение:
Высота, проведённая из прямого угла делит треугольник на два прямоугольных треугольника, у которых равные углы.
Угол между медианой и высотой, проведённых из вершины прямого угла равен разнице острых углов треугольника.
Угол между биссектрисой и высотой, проведённых с вершины прямого угла равен половине разницы острых углов треугольника.
Квадрат высоты, проведённой к гипотенузе, равен произведению проекций катетов на гипотенузу.
Если высота, проведённая на гипотенузу, делит её на отрезки, разница которых равна одному из катетов треугольника, то острые углы относятся как 1:2.
Высота, которая опущена из прямого угла треугольника, равна произведению катетов, поделённому на гипотенузу.
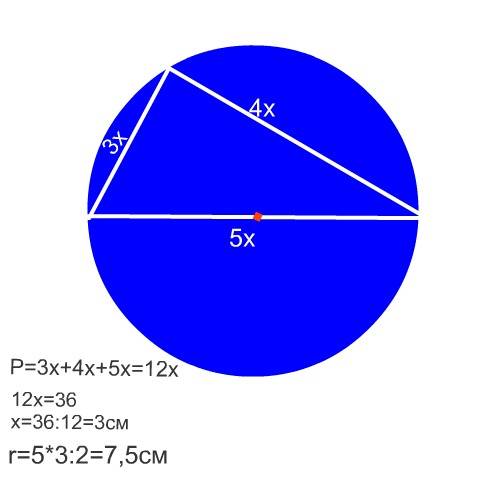
Гипотенуза этого прямоугольного треугольника является диаметром окружности.
Так как отношение катетов 3:4, то гипотенуза в этом отношении будет 5,
т.е все стороны треугольника относятся как 3:4:5, поскольку этот треугольник - египетский.
Примем коэффициент отношения сторон за х
тогда его периметр равен
3х+4х+5х=12х
Коэффициент равен 36:12=3
Диаметр круга
3*5=15 см
Радиус 15:2=7,5 см
-------------------------------
Боковую сторону можно найти через синус угла при вершине треугольника.
Он равен 180-2а
х=h: sin(180-2а)
гипот.=64+36=100
AB=10
sinA=BC/AB
sinA=6/10
sinA=0.6