Объяснение:
Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
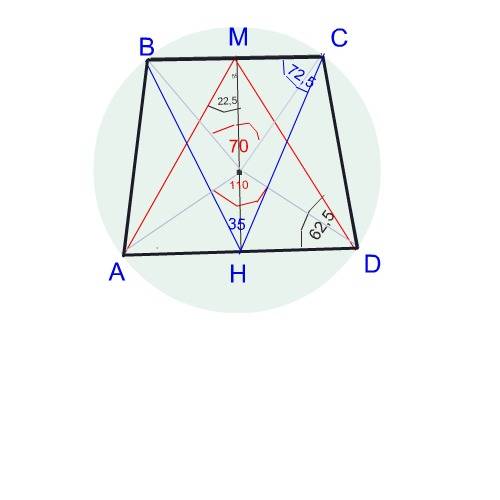
Пусть плоскость проведённая через B, D и серединную точку M ребра B₁C₁ пересекается с плоскостью B₁C₁А₁ по прямой MN. M∈B₁C₁, N∈D₁C₁.
⇒MN||BD⇒BDNM-трапеция
BD||B₁D₁; MN||BD⇒MN||B₁D₁
MN-средняя линия треугольника B₁C₁D₁
ABCDA1B1C1D1- правильный прямоугольный параллелепипед⇒ABCD-квадрат, а боковые грани прямоугольники.
B₁M=0,5B₁C₁=ND₁, DD₁=BB₁, ∠MB₁B=∠ND₁D=90°⇒ΔMB₁B=ΔND₁D⇒MB=ND⇒
⇒BDNM-равнобедренная трапеция. Ч.Т.Д.
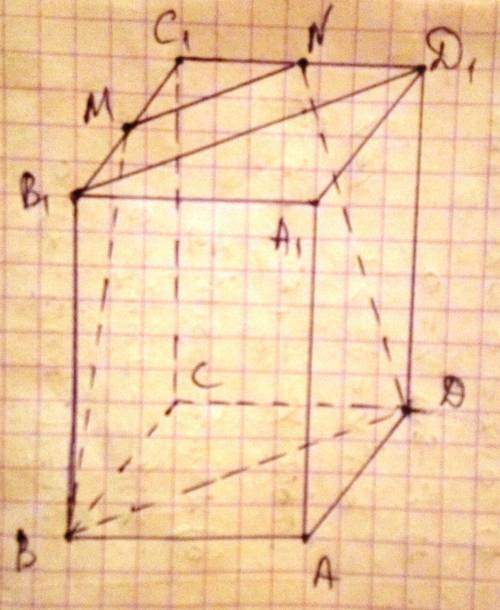
Рисуем трапецию в окружности.
Дополним рисунок треугольниками АМD и ВНС.
Углы при вершинах этих треугольников равны половине центральных углов ( под которыми видны из центра окружности основания трапеции)
Путем несложных вычислений находим углы треугольников DМН и МНС
Для решения применена теорема синусов.
Синусы найденных углов
72,5=0,9537
62,5=0,8870
22,5=0,3826
17,5=0.3007
---------------------------------
МН:sin 62,5=8:0,887=9,019
DН=9,019∙ sin22,5=3,4507
AD=6,9
-------
МН:sin 72,5=8:0,9537=8,3884
СМ=8,3884∙sin17,5=2,52
ВС=5,04
Ясно, что значения длин сторон округленные.
-------------
Площадь трапеции равна произведению полусуммы оснований на ее высоту.
S ABCD=8(6,9+5,04):2=95,52 (?)³