Из ∆АВС: ∠В=30, ∠А=60°
Из ∆АВД: ∠АВД=15°, ∠АДВ=105°
Из ∆СВД: ∠СВД=15°, ∠ВДС=75°
Объяснение:
Сумма смежных углов составляет 180°, а ∠ВАЕ смежный с ∠ВАС, значит
∠ВАС=180–∠ВАЕ=180–120=60°
Рассмотрим ∆АВС, он прямоугольный, с прямым ∠С=90°. Сумма острых углов прямоугольного треугольника равна 90°, тогда
∠АВС=90–∠ВАС=90–60=30°
Из условия известно что ВД - биссектриса и делит ∠В пополам, поэтому
∠АВД=∠СВД=30÷2=15°
Рассмотрим ∆АВД, в нём ∠ВАД=60°, ∠АВД=15°. Сумма углов треугольника составляет 180°, значит
∠АДВ=180–∠ВАД–∠АВД=180–60–15=105°
∠ВДС смежный с ∠АДВ, тогда
∠ВДС=180–105=75°
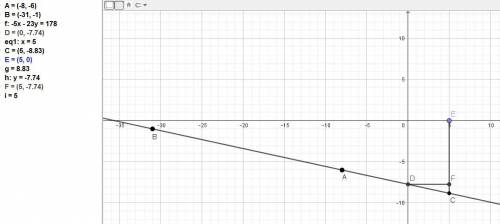
Угловой коэффициент прямой равен: к = Δу/Δх.
к = (-1-(-6))/(-31-(-8)) = 5/(-23).
Он даёт прирост функции на единицу прироста аргумента.
Δу(С) = 5*(-5/23) = -25/23. Это прирост функции от 0 до 5.
Вектор АВ = (-23; 5).
Воспользуемся формулой канонического уравнения прямой:
(x - xa) / (xb - xa) = (y - ya) / (yb - ya).
Подставим в формулу координаты точек:
(x - (-8)) / ((-31) - (-8)) = (y - (-6)( / ((-1) - (-6)).
В итоге получено каноническое уравнение прямой:
(x + 8) / (-23) = (y + 6) /5.
Из уравнения прямой в каноническом виде получим уравнение прямой с угловым коэффициентом:
y = (-5 / 23)x - (178 / 23).
Подставим координату х в полученное уравнение.
y = (-5 / 23)*5 - (178 / 23) = -203/23.
ответ: точка С(5; (-203/23).
из серии "как нетрудно догадаться")))
первая мысль, которая должна бы появиться: раз есть окружность -- нужно искать углы...вписанные и центральные... искать равные углы...
искать дуги, на которые углы опираются...
центр описанной окружности = точка пересечения серединных перпендикуляров к сторонам треугольника)))
треугольник ВОА равнобедренный по построению и серединный перпендикуляр к стороне ВС -- это биссектриса=медиана=высота)))
угол ВОА -- центральный, опирающийся на дугу ВА,
угол ВСА -- вписанный, опирающийся на ту же дугу)))
вывод: ВОА = 2*ВСА
в равнобедренном треугольнике ВОА -- ВК это высота (по условию))) и
серединный перпендикуляр к основанию -- тоже высота))
получили два прямоугольных треугольника с общим углом ВАО
значит третьи углы в этих треугольниках равны)))
угол АВК будет равен половине угла АОВ: АОВ = 2*АВК,
т.е. ВСА = АВК
а теперь если вернуться к данному треугольнику АВС, то "нетрудно заметить",
что треугольники АВС и АВD -- подобны
у них угол ВАС -- общий, и два острых угла равны: АВD = ВСА
запишем пропорцию:
АВ / АС = AD / AB
AD = AB*AB / AC = 8*8 / 64 = 1
CD = 64 - 1 = 63