1)
Объяснение:
1) Все диаметры окружности равны между собой.
Верно.
Диаметр в два раза больше радиуса, а все радиусы окружности равны.
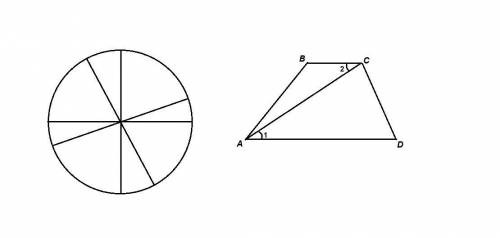
2) Диагональ трапеции делит ее на два равных треугольника.
Неверно.
Диагональ параллелограмма делит его на два равных треугольника, в трапеции эти треугольники очевидно не равны:
для ΔАВС и ΔADC АС - общая сторона, ∠1 = ∠2 как накрест лежащие при пересечении AD║ВС и секущей АС, но AD ≠ ВС.
3) Площадь любого параллелограмма равна произведению длин его сторон.
Неверно.
Площадь параллелограмма равна произведению двух соседних сторон на синус угла между ними.
Если две стороны одного треугольника пропорциональны
двум сторонам другого треугольника и углы,
заключенные между этими сторонами, равны,
то такие треугольники подобны)))
из равенства углов ВСА и ВDA и равенства вертикальных углов ВOC и AOD
((точка О -- точка пересечения диагоналей АС и BD выпуклого 4-угольника)))
следует, что треугольники ВОС и АОD подобны по двум углам...
следовательно, верна пропорция:
OD / OC = AO / OB
равносильная этой пропорция тоже очевидно верна:
OD / АO = OС / OB (((т.к. OD*OB = OC*AO ---> OD = OC*AO / OB...)))
а это отношение можно прочесть так:
две стороны треугольника COD
пропорциональны двум сторонам треугольника АОВ и
углы COD и АОВ между этими сторонами равны ((как вертикальные))),
следовательно треугольники AOB и COD -- подобны.
Из подобия следует равенство углов)))
т.е. против OD -- угол OCD и против АО -- угол АВО
---> углы против соответственных сторон -- равные углы)))