«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия». Эти слова, сказанные великим французским архитектором Ле Корбюзье в начале XX века, очень точно характеризуют и наше время. Мир, в котором мы живем, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Так же, как самое большое здание складывается из маленьких кирпичей, так и сложные геометрические фигуры составляются из простейших геометрических фигур.
Какие геометрические фигуры изучаются в курсе геометрии 8 класса? (Четырехугольники)
Итак, тема нашего урока «Четырехугольники». На уроке мы обобщим знания, умения и навыки по этой теме. Для этого необходимо повторить теоретические сведения, а также проведем тестирование ваших знаний о четырехугольниках, решим основные типы задач, проведем небольшое исследование.
Сегодня на уроке вам предстоит оценить себя самим.
Перед вами на партах лежит таблица, которую вы в конце урока заполните плюсами и минусами за каждый вид вашей деятельности .
Вспомним с вами основные понятия по теме «Четырехугольники». Для этого я буду задавать вопрос, а вы по цепочке будете на них отвечать.
Что называется четырехугольником?
Перечислите основные виды четырехугольников?
Сформулируйте определение параллелограмма.
Назовите основные свойства параллелограмма.
Что называется прямоугольником?
Какое новое свойство у прямоугольника?
Что такое ромб?
Сформулируйте особое свойство ромба.
Что называется квадратом?
Перечислите свойства квадрата.
Что такое трапеция?
Назовите виды трапеции.
Учебно-познавательная деятельность
Сведения из истории четырехугольников.
История четырехугольников
В древних египетских и вавилонских документах встречаются следующие виды четырехугольников: квадраты, прямоугольники, равнобедренные и прямоугольные трапеции. В частности, в клинописных математических табличках встречаются прямоугольные треугольники, рассеченные параллелями к одному из катетов на прямоугольной трапеции.
Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом
Термин «параллелограмм» греческого происхождения, который был введен Евклидом. Он называл параллелограмм “параллельно-линейной площадью”. Слово parallhlogrammou составлено из parallhloz и grammh-- “линия” это слово дало основу для термина “параллелограмм”.
Понятие параллелограмма и некоторые его свойства были известны пифагорейцам.
В «Началах» Евклида доказывается следующая теорема: в параллелограмме противоположные стороны равны и противоположные углы равны, а диагональ разделяет его пополам. Евклид не упоминает о том, что точка пересечения диагоналей параллелограмма делит их пополам. Он не рассматривает ни прямоугольника, ни ромба. Полная версия параллелограммов была разработана к концу средних веков и появилась в учебниках лишь с 17 века. Все теоремы о параллелограммах основываются непосредственно или косвенно на аксиоме параллельности Евклида.
Первые геометры, в том числе и Евклид, мыслили прямоугольник, вписанный в круг.
Ромб — это параллелограмм, у которого все стороны равны.
Слово «ромб» тоже греческого происхождения, оно означало в древности вращающееся тело, веретено, юлу. Образ ромба был связан первоначально с сечением, проведенным в обмотанном веретене.
Есть и другое значение.Термин «ромб» образован от греч. ρομβος — «бубен». Если сейчас бубны в основном делают круглой формы, то раньше их делали как раз в форме квадрата или ромба. Кстати, название карточной масти бубны, знаки которой имеют ромбическую форму, происходит ещё с тех времён, когда бубны не были круглыми.
Слово «ромб» впервые употребляется у Герона и Паппа Александрийского.
Квадрат – это прямоугольник, у которого все стороны равны.
Термин «квадрат» происходит от латинского quadratum (quadrare- сделать четырехугольным), перевод с греческого –четырехугольник.
Трапеция – это четырёхугольник, где две стороны параллельны, а две другие не параллельны.
Трапеция – слово греческое, означавшее в древности «столик». В «Началах» термин «трапеция» применяется не в современном, а в другом смысле: любой четырехугольник (не параллелограмм). «Трапеция» в нашем смысле встречается впервые у древнегреческого математика Посидония (1век). В средние века трапецией называли, по Евклиду, любой четырехугольник (не параллелограмм); лишь в 18 веке это слово приобретает современный смысл.
Тестирование.
Объяснение:
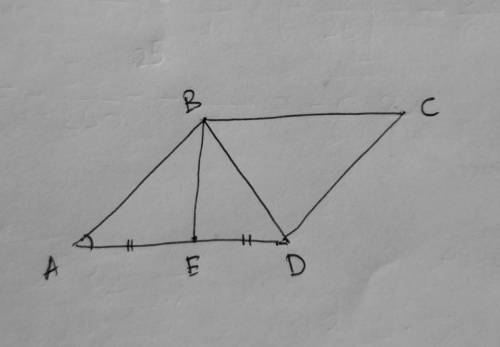
Дано:
параллелограмм ABCD
угол BAE = 60°
AE = ED
P(ABCD) = 48
Найти: BD
P = 2(a + b) = 2AD + 2AB = 48
AD + AB = 24
треугольник ABE — прямоугольный, а значит сумма углов равна 180°.
угол BAE = 60° по заданию,
угол AEB = 90°, так как BE — высота и перпендикулярна AD,
угол ABE = 180° – 60° – 90° = 30°
По свойству прямоугольного треугольника, катет, лежащий напротив угла 30°, равен половине гипотенузе:
AE = AB / 2
AE = ED = AD / 2 по заданию
AD / 2 = AB / 2 =>
AD = AB =>
параллелограмм ABCD — равносторонний =>
AD + AB = 24
2*AD = 24
AD = 12
Треугольник ABD — равнобедренный, значит
AB = BD = 12
ответ: 12
так как
Подставим
По формуле радиус описанной окружности равен
Так как
Площадь равна сумме площадей треугольников