Правильный четырехугольник - это квадрат.
Радиус вписанной в него окружности равен половине стороны. ⇒
а=2r
P=4•2r=8r
C=2πr
P/C=8r/2πr=4/π, и это величина для квадрата постоянная.
По данным задачи:
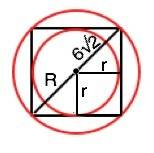
Радиус окружности, описанной около квадрата, равен половине диагонали квадрата.
Тогда диагональ квадрата 2•R=12√2
Сторона квадрата – катет равнобедренного прямоугольного треугольника с гипотенузой 12√2 и острыми углами 45°
а=12√2•sin45°=6√2•√2:2=12
Р=4•12=48
Радиус вписанной окружности r=12:2=6
С=2•p•6=12π
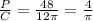
Дана равнобедренная трапеция ABCD.Линии при основании равны 6 см и 12 см.Угол при основании равен 60 градусам.Найти периметр и боковые стороны трапеции.
в трапеции опустим 2 перпендикуляра bb1 и cc1 угол при основании a он равен углу d так как равнобедренная трапеция ab=cd треугольник abb1=треуг сс1d по 2 признаку ( угол a=d, ab=dc ,2 угла равны так как они по 90 перпендикуляры) значит ab1=c1d=3 см ab=6 потаму что ab1 лежит против угла 30 градусов он равет половине гипотенузы (ab1=3 то ab=6) ab=cd=6 см Р abcd=6+6+6+12=30 ответ р=30 а стороны равны ab=6 см cd=6см
параллелепипед прямоугольный --т.е. все грани -- прямоугольники)))
диагональ параллелепипеда образует угол 45 с боковым ребром --т.е.
в прямоугольном треугольнике с гипотенузой = 10 см и
катетами:
--высота параллелепипеда (h) и
--диагональ основания ( = √(a² + b²) )))
острый угол = 45 градусов)))
т.е. этот треугольник равнобедренный и высота параллелепипеда =
диагонали основания
h² + h² = 10²
h² = 50
h = 5√2
диагональ параллелепипеда образует угол 30 с плоскостью боковой грани --т.е.
в прямоугольном треугольнике с гипотенузой = 10 см и
катетами:
--длина основания (b например)))
--диагональ боковой грани ( = √(a² + h²) )))
острый угол = 30 градусов)))
катет против угла 30 градусов = половине гипотенузы)))
b = 10/2 = 5
по т.Пифагора
10² = 5² + a² + h² = 5² + a² + 50
a² = 25
a = 5
V = 5*5*5√2 = 125√2