Площадь боковой поверхности равна 756 дм².
Площадь полной поверхности равна 1145 дм².
Объяснение:
Площадь боковой стороны усеченной пирамиды равна площади равнобочной трапеции с основаниями 17 и 10 дм и высотой, равной апофеме 14 дм.
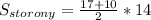
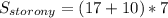
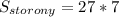
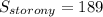 дм².
дм².
В площади боковой стороны таких трапеций четыре.
Значит
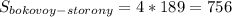 дм².
дм².
Площадь полной поверхности равна сумме площади боковой поверхности и площадей оснований.
Площадь меньшего основания равна площади квадрата со стороной 10 дм
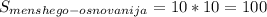 дм².
дм².
Площадь большего основания равна площади квадрата со стороной 17 дм
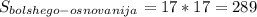 дм².
дм².
Теперь надо сложить все эти три площади
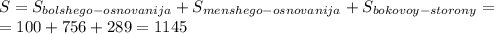
дм².
См. Объяснение
Объяснение:
Задание
Из точки, которая находится на расстоянии 8 см от прямой, проведены к ней две наклонные, образующие с прямой углы 30 и 45 градусов. Найдите расстояние между основаниями наклонных, сколько решений имеет задача.
Вариант 1 - основания наклонных находятся по разные стороны от проекции точки на данную линию.
1) Длина проекции наклонной, образующей с ней угол 30°, равна:
8 · ctg 30° = 8√3 см
2) Длина проекции наклонной, образующей с ней угол 45°, равна:
8 · ctg 45° = 8 см
3) Расстояние между основаниями наклонных:
8√3 + 8 = 8 (√3 + 1) см ≈ 8 · (1,732 + 1) = 8 · 2,732 ≈ 21,86 см
Вариант 2 - основания наклонных находятся по одну сторону от проекции точки на данную линию.
1) Длина проекции наклонной, образующей с ней угол 30°, равна:
8 · ctg 30° = 8√3 см
2) Длина проекции наклонной, образующей с ней угол 45°, равна:
8 · ctg 45° = 8 см
3) Расстояние между основаниями наклонных:
8√3 - 8 = 8 (√3 - 1) см ≈ 8 · (1,732 - 1) = 8 · 0,732 ≈ 5,86 см
ответ: в данной задаче - 2 решения:
1) если основания наклонных находятся по разные стороны от проекции точки на данную линию, то расстояние между ними равно
8(√3+1) см ≈ 21,86 см;
2) если основания наклонных находятся по одну сторону от проекции точки на данную линию, то расстояние между ними равно
8(√3-1) см ≈ 5,86 см.
1) площади треугольников ABK и CDK равны.
В самом деле, если положить угол AKB = Ф, то
Sadk = AK*BK*sin(Ф)/2; Scdk = CK*DK*sin(Ф)/2; и BK/DK = CK/AK; то есть BK*AK = CK*DK; Поэтому площадь трапеции равна S = Sakd + Sbkc + 2*Sakb;
2) из вершины C проводится прямая CE II BD; точка E лежит на продолжении AD. Ясно, что DBCE - параллелограмм, и DE = BC; то есть AE = AD + BC;
Следовательно, площадь треугольника ACE равна площади трапеции ABCD, поскольку у них общая высота (расстояние от точки C до AD) и одинаковые средние линии.
Sabcd = Sace = S;
3) треугольник ACE очевидно подобен треугольникам AKD и BKC; причем, если сравнивать соответствующие стороны, то
BK/CE = 1/5; DK/CE = 4/5; (это так в условии ЗАДАНО :) )
Отсюда Sbkc = S*(1/25); Sakd = S*(16/25);
4) S = 2*24 + S*(1/25) + S*(16/25);
S = 150;