Возьмем две точки на прямой, например (0;6) и (2;4). найдем две точки, симметричные точкам (0;6) и (2;4) относительно точки (1;-2)
Пусть это будут точки (х₁;у₁) (х₂;у₂) соответственно.
тогда х₁=2*1+0=2; у₁=2*(-2)-6=-10. Нашли точку (2;-10).
найдем теперь х₂=2-2=0; у₂=2*(-2)-4=-8. нашли точку (0; -8)
В уравнение у=кх+в подставим полученные точки и решим систему двух уравнений с двумя переменными.
2к+в=-10
0к+в=-8
из второго уравнения в= -8, подставим в первое, получим 2к=-10+8, к = -1, искомое уравнение примет вид у =-х-8
ответ у =-х-8
Возьмем две точки , лежащие на исходной прямой. Пусть это точка (0;6) и (2;4). Построим точки, симметричные данным относительно точки А(1;-2), для этого учтем А будет серединой отрезка, соединяющего точку (о;6) с ей симметричной точкой (х₁;у₁).
(0+х₁)/2=1, откуда х₁= 2
(6+у₁)/2= -2, откуда у₁=-10, Получили точку (2;-10) симметричную точке (0;6) относительно точки А(1;-2).
Аналогично найдем еще одну искомой прямой. Пусть это будет точка
(х₂;у₂), которая симметрична точке (2;4) относительно А(1;-2)
(2+х₂)/2=1; откуда х₂=0
(4+у₂)/2=-2; откуда у₂=-8
получили еще одну точку (0;-8), симметричную точке (2;4) относительно точки А(1;-2)
Составим теперь уравнение прямой, проходящих через найденные точки (2;-10) и (0;-8)
у = кх +в, подставим в это уравнение прямой сначала одну, потом другую точку, получим систему двух уравнений. ИЗ НЕЕ НАЙДЕМ К И В. И отыщем искомую прямую.
2к+в=-10
0*к+в=-8 из второго уравнения в =-8, тогда из первого 2к=-2, к = -1, искомое уравнение прямой примет вид у = -х-8
ответ у = -х-8
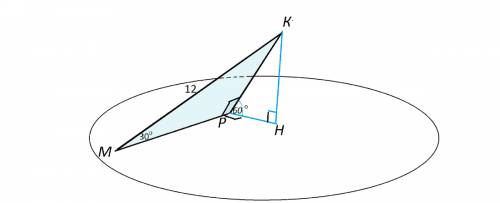
Расстояние от точки до плоскости измеряют перпендикулярным отрезком.
Это отрезок КН прямоугольного треугольника КРН. КР, противолежащая углу 30° треугольника КРМ, равна половине КМ и равна 6 см.
КН=КР*sin ∠КРН=КР*sin (60)=3√3
2)
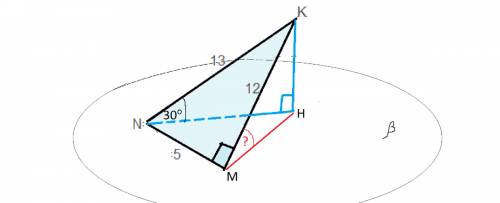
Плоскость β проходит через сторону MN треугольника MKN. Сторона KN образует с плоскостью β угол 30°. Найдите синус угла между плоскостями β и MKN, если MK=12см, KN=13см, MN=5см
Обратим внимание на отношение сторон треугольника -12:13:5. Это отношение прямоугольного треугольника из Пифагоровых троек. ( Можете проверить).
Точка К проецируется на плоскость β в точке Н, а КН перпендикулярна β . Из треугольника КNH найдем КН .
Она равна половине КH как катет, противолежащий углу 30°
Т.к. наклонная КМ перпендикулярна МN, то ее проекция также перпендикулярна МN.
Угол. синус которого надо найти, ограничен отрезками КМ и МН.
Т.е. это угол КМН.
sin ∠КМН=KH:KM=6,5:12=0,541(6)
-----------
[email protected]