Сумма острых углов прямоугольного треугольника равна 90.Пусть один острый угол х, тогда второй (х+60), составим уравнение:
х+х+60=90
2х=30
Х=30:2
Х=15-один острый угол
90-15=75-другой острый угол
ответ:15;75.
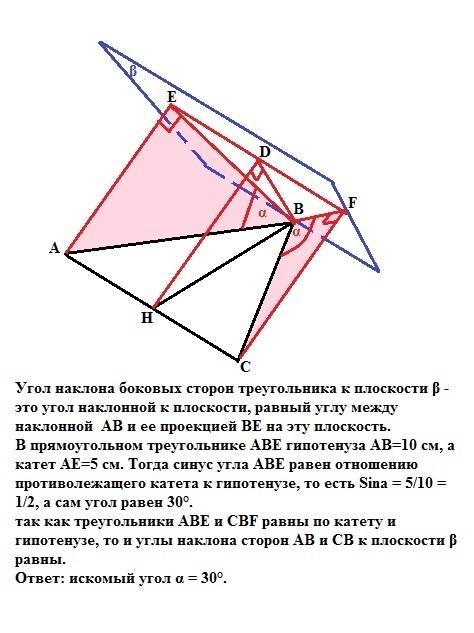
Треугольник АВС равнобедренный с основанием АС. Высоту этого треугольника ВН найдем через площадь: h= 2S/а, где S - площадь, а - сторона, к которой проведена высота. ВН = 2*48/12 = 8 см. Боковые стороны АВ и ВС равны по Пифагору √(ВН²+АН²) = √(8²+6²) =10 см.
Опустим перпендикуляры из точек А, Н и С на плоскость β. Эти перпендикуляры АЕ, НD и СF равны расстоянию от прямой АС до плоскости β (5 см - дано) в силу параллельности плоскости β прямой АС.
Угол наклона боковой стороны АВ треугольника к плоскости β - это угол наклонной АВ к плоскости, равный углу между наклонной АВ и ее проекцией ВЕ на эту плоскость.
В прямоугольном треугольнике АВЕ гипотенуза AВ=10 см, а катет АЕ=5 см. Синус угла АВЕ равен отношению противолежащего катета к гипотенузе, то есть Sina = 5/10 = 1/2, а сам угол равен 30°.
Так как треугольники АВЕ и СВF равны по катету и гипотенузе, то и углы наклона сторон АВ и СВ к плоскости β равны.
ответ: искомый угол α = 30°.
Сумма углов треугольника равна 180 градусов, тогда 180-90=90 градусов - градусная мера двух углов. Допустим, один угол равен х, тогда второй х+60. Известно, что их сумма равна 90
2х=90-60
2х=30
х=30:2
х=15 - 1 угол
15+60=75 -2 угол