
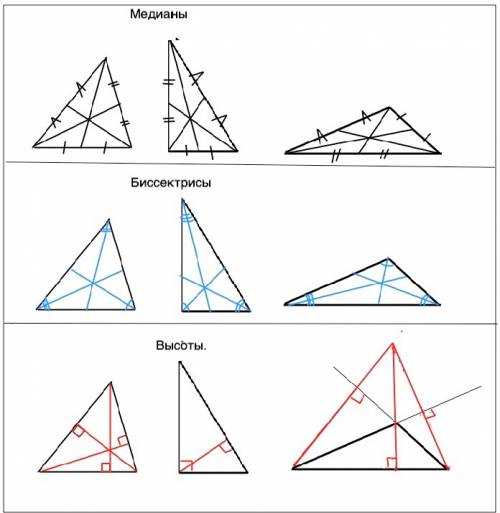
Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.
Биссектрисы треугольника пересекаются в одной точке, расстояние от которой до сторон треугольника одинаково и является центром вписанной окружности.
Высоты треугольника пересекаются в одной точке. Точка пересечения высот остроугольного треугольника находится внутри него. Точка пересечения высот прямоугольного треугольника - вершина прямого угла.
Высоты тупоугольного треугольника, проведенные из вершин его острых углов, проходят вне его и пересекают продолжения сторон. Точка пересечения высот тупоугольного треугольника находится вне треугольника.
ABC - прямоугольный треугольник; ∠C = 90
BC = 12 (см); tg ∠A = 3/4
Найти: АС
Решение:
tg ∠A - отношение противолежащего катета к прилежащему катету
tg ∠A = BC /AC = 3/4
Так как видно что ВС = 3 см, домножим на 4
tg ∠A = 3/4 = 12/16
12 см - сторона ВС - по условию
16 см - сторона АС
ответ: АС = 16 (см).