Медианы треугольника пересекаются в одной точке, и точкой пересечения делятся в отношении 2:1, считая от вершины.
следовательно ВМ:МК=2:1.
У ΔАМК и ΔАВМ одна и та же высота АН - перпендикуляр, проведенный из вершины А к прямой ВК, содержащей стороны ВМ и МК этих треугольников.
Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты), следовательно:
Samk/Sabm=1/2 следовательно:
12/Sabm=1/2 следовательно:
24=Sabm.
Sabk=24см²+12см²=36см²
медиана ВК делит ΔАВС на два равновеликих т.е Sabk = Skbc.
⇒
Sabc=36*2=72см².
ответ: 72см²
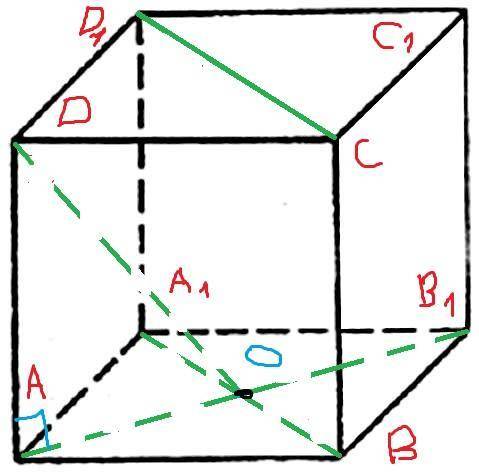
DO и CD₁ - скрещиваются, но А₁В ║ CD₁ ⇒ угол между прямыми DO и CD₁ равен углу между прямыми DO и А₁В. Пусть ребро исходного куба равно единице: АВ = 1, тогда диагональ грани равна корню из двух: А₁В = √2. Рассмотрим ΔDАO – прямоугольный (DА ⊥ АO), по теореме Пифагора: DO² = АO² + DА², АО = 0,5*АВ₁ = 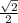 ⇒
⇒
DO² = 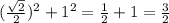 .
.
Далее рассмотрим ΔDOВ, где ∠DOВ = углу между прямыми DO и А₁В =
= углу между прямыми DO и CD₁. При этом DВ = √2 как диагональ квадрата с единичной стороной, ОВ = 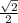 , DO² =
, DO² = 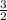 .
.
По теореме косинусов: DВ² = DO² + ОВ² – 2 · DO · ОВ · сos(∠DOВ) ⇒
√2² = 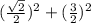
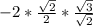 * сos(∠DOВ) ⇒
* сos(∠DOВ) ⇒
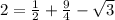 * сos(∠DOВ)) ⇒
* сos(∠DOВ)) ⇒
√3*сos(∠DOВ) = 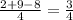 ⇒ сos(∠DOВ) =
⇒ сos(∠DOВ) = 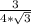 =
= 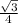 ⇒
⇒
∠DOВ = углу между прямыми DO и CD₁ = arccos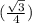
2) Для этого пункта я не буду делать отдельный чертеж. В задаче задан радиус сферы, описанной около ПРАВИЛЬНОГО тетраэдра. Он равен √66;
Связь между радиусом R и ребром тетраэдра a такая R = a*√6/4;
Я не буду подробно показывать, как это получается - это отдельная задача. Но - в качестве бонуса НЕ ПОДРОБНО и БЕЗ РИСУНКА расскажу, как проще всего это найти. Предположим, задан куб ABCDA1B1C1D1 с ребром длины a√2/2. Тогда фигура с вершинами AB1CD1 - правильный тетраэдр с ребром a (все ребра тетраэдра - диагонали граней куба). Ясно, что сфера, проходящая через вершины тетраэдра, пройдет через все вершины куба, то есть это сфера, описанная вокруг куба с ребром b = a√2/2; радиус такой сферы равен половине большой диагонали куба, то есть R = b√3/2 = a√6/4;
По условию a√6/4 = √66; a = 4√11;
3) Итак, ребро тетраэдра равно a = 4√11; вот теперь можно НАЧАТЬ решать задачу.
Сечение EDQ - треугольник с постоянной стороной ED. Поэтому минимальная площадь будет, если расстояние от Q до ED равно расстоянию между скрещивающимися прямыми ED и BC. То есть НЕ НУЖНО находить, где именно расположена точка Q. Надо найти расстояние между ED и BC, это и будет значение высоты треугольника EDQ к стороне ED в "минимальном сечении"
(это практически всё решение, дальше одни технические действия).
На чертеже EF II BC; поэтому плоскость EDF II BC. Поэтому надо найти расстояние от точки N (середина BC) до плоскости EDF.
Так как плоскость ADN перпендикулярна BC и EF, то задача "перемещается в плоскость" AND. В РАВНОБЕДРЕННОМ треугольнике ADN (AN = DN) надо найти расстояние от вершины N до медианы DG;
4) Стороны AN = DN = a√3/2; высота к AN тоже известна - это высота всего тетраэдра DO = a√(2/3); поэтому площадь ADN равна AN*DO/2 = a^2*√2/4;
Площадь треугольника DGN равна половине площади ADN, то есть a^2*√2/8;
5) осталось найти DG; по известной формуле для медианы
(2*DG^2) = 2*(AD^2 + DN^2) - AN^2 = 2*a^2 + (a*√3/2)^2 = a^2*11/4;
DG = a*√11/4; (единственное целое число у меня вылезло :))
6) NK*DG/2 = Sdgn; то есть a^2*√2/8 = NK*a√11/4; NK = a√(2/11);
7) Искомая минимальная площадь сечения равна ED*NK/2 = (a√3/2)*(a√(2/11))/2 = (a^2/4)*√(6/11) = 44√(6/11);
Я вполне мог ошибиться в числах - у меня нет времени все проверять, это вы уж сами. Смысл решения вот такой...