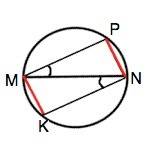
Вписанные углы РMN и KNM опираются на равные хорды. Следовательно, дуги, стягиваемые этим хордами, равны. Вписанные углы, опирающиеся на равные дуги (или на равные хорды), равны.
∠РMN=∠KNM
Проведем хорды МР и КN.
В треугольниках MPN и MKN вписанные ∠Р = ∠К (опираются на диаметр).⇒
Прямоугольные ∆ МРN=∆ MKN по острому углу и общей гипотенузе.
Отсюда следует равенство PNM=KMN
Эти углы - накрестлежащие при пересечении РN и MK секущей MN.
Если при пересечении двух прямых секущей накрестлежащие углы равны. эти прямые - параллельны. Доказано.
Для начала нарисуем произвольную трапецию АВСD и через точку Е проведем прямую EF параллельную основаниям трапеции
Найдем площадь треугольника CEF, которая равна EF*h1/2, затем найдем площадь треугольника DEF, которая также равна EF*h1/2.
Площадь треугольника ЕСD равна сумме площадей этих треугольников
EF*h1/2 + EF*h1/2 = EF*h1
EF - средняя линия трапеции и равна она половине суммы оснований, а именно (а+в)/2;
высота h1 равна половине высоты трапеции, а именно h/2.
Осталось только подставить значения
EF*h1 = (а+в)/2*h/2 = (а+в)*h/4 и сравнить
площадь трапеции формула
Площадь треугольника ЕСD равна половине площади трапеции, что и требовалось доказать.
Путь по течению = 45 км
Скорость против течения = (x-2) км/ч
Скорость по течению = (x+2) км/ч
Общее время = 14 ч
S=v*t
t=S/v
45/(x+2) + 45/(x-2) = 14
(45(x-2)+45(x+2)) / ((x+2)(x-2)) = 14
(45x-90+45x+90) / (x^2-2x+2x-4) = 14
(90x) / (x^2-4) = 14
90x = 14(x^2-4)
90x=14x^2-56
14x^2-90x-56=0
D=(-90)^2-4*14*(-56)=8100+3136=11236
x1=(90+106)/28=196/28=7 (км/ч)
x2=(90-106)/28=-16/28=-4/7 - не удовлетворяет условию задачи
ответ: собственная скорость лодки 7 км/ч
проверка:
S1=45 км
v1=7-2=5 км/ч - против течения
S2=45 км
v2=7+2=9 км/ч - по течению
t=14
45/5 + 45/9 = 14
9+5=14
14=14