а) BC1 || AD1, поэтому угол между прямыми AB1 и BC1 равен углу между AB1 и AD1.
ребро куба равно а, поэтому (так как грани куба - квадраты), то AB1=AD1=B1D1, а значит треугольник AB1D1 - правильный(равносторонний),
углы равностороннего треугольника равны 60 градусов,
значит искомый угол между прямыми AB1 и BC1 равен 60 градусов
б) так как В1С1 - перпендикуляр с точки С1 на грань АА1В1В, то угол между прямой AC1 и гранью AA1B1B равен углу В1АС1
(треугольник АВ1С1 - прямоугольным с прямым углом АВ1С1)
по свойству диагонали квадрата 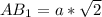
по свойству диагонали куба 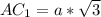
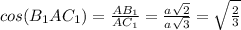
угол В1АС1 равен arccos корень(2/3)т.е.
угол между прямой AC1 и гранью AA1B1B равен arccos корень(2/3) градусов
118°, 118°, 62°, 62°
Объяснение:
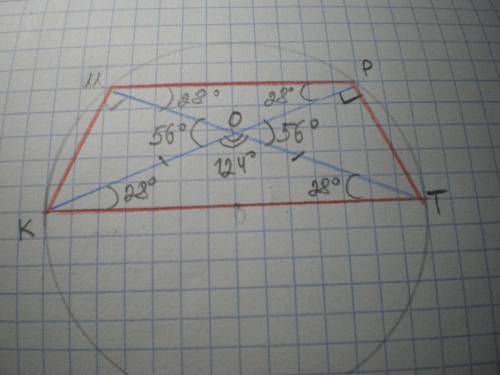
Дано: КМРТ - трапеция, МК=РТ, КТ=D (окружности), КР и МТ - диагонали, ∠РОТ=∠МОК=56°. Найти ∠К, ∠М, ∠Р, ∠Т.
Решение: ΔКМТ=ΔТРК, т.к. КР=МТ как диагонали равнобедренной трапеции, КМ = РТ по условию, сторона КТ - общая. Значит, ∠ОКТ=∠КТО.
∠КОТ=180-56=124°; ∠ОКТ=∠КТО=(180-124):2=28°.
ΔМОР; ∠МРО=∠ОМР=∠ОКТ=∠КТО=28° как внутренние накрест лежащие при МР║КТ и секущих МТ и КР.
∠КМТ=∠КРТ=90° как углы, опирающиеся на диаметр окружности.
∠М=∠Р=90+28=118°
∠К=∠Т=180-118=62° по свойству углов трапеции, прилежащих к боковой стороне
Удивительно :), но задача решается на много проще, если к уже заявленным точкам A B E F, через которые проходит сфера, добавить еще точку С и точку G - центр грани BCD.
Сечения сферы параллельными плоскостями ABC и EFG - окружности, описанные вокруг правильных треугольников ABC (с стороной 2, радиус описанной окружности 2/√3)) и EFG.
Само собой, центры этих треугольников (и окружностей) тоже лежат на высоте тетраэдра из точки D.
Расстояние между плоскостями этих сечений-окружностей равно d = H/3, где H = 2*√(2/3); - высота тетраэдров, то есть d = (2/3)*√(2/3);
Стороны треугольника EFG соединяют середины линий, проведенных через центры боковых граней параллельно основанию. То есть они равны (1/2)*(2/3)*2 = 2/3; радиус описанной окружности равен r2 = r1/3;
Таким образом, задача теперь звучит так. Надо найти радиус сферы, если известны радиусы двух параллельных сечений этой сферы r1 и r2 и расстояние между ними d;
Пусть x - расстояние от центра сферы до плоскости ABC, R - радиус сферы.
x^2 + r1^2 = R^2;
(x + d)^2 + r2^2 = R^2;
Откуда легко найти x = (r1^2 - r2^2 - d^2)/(2*d); легко найти x = √(2/3); то есть это половина высоты тетраэдра.
То есть центр сферы лежит ниже плоскости ABC на расстоянии H/2 от неё.
R = √2;