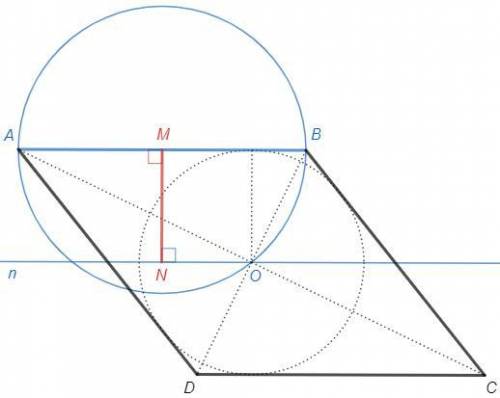
Построим ромб по стороне a и радиусу вписанной окружности r.
1) AB=a
2) проведем прямую n, параллельную AB, на расстоянии r
Для этого
- построим перпендикуляр к AB
- отложим на нем отрезок MN=r
- через точку N проведем прямую n, перпендикулярную MN
3) построим окружность на отрезке AB как на диаметре
4) пересечение окружности и прямой n = точка O
Угол AOB - прямой, так как опирается на диаметр AB.
Диагонали ромба пересекаются под прямым углом.
Диагонали ромба являются биссектрисами, точка их пересечения - центр вписанной окружности - удалена от стороны AB на радиус.
Таким образом, точка O - центр пересечения диагоналей ромба.
5) построим вершины С и D ромба, симметричные A и B относительно точки O.
Для этого
- проведем прямую BO
- отложим отрезок DO=OB итд
Пусть х - коэффициент пропорциональности, тогда один катет равен 15х, второй 20х.
Так как гипотенуза равна 15+20=35, то по теореме Пифагора
(15х)²+(20х)²=35²
225х²+400х²=1225
625х²=1225
х²=1,96
х=1,4
Один катет 15х=15·1,4=21, второй катет 20х=20·1,4=28
ответ. 21 см; 28 см.