Pabcd = 40 дм.
Объяснение:
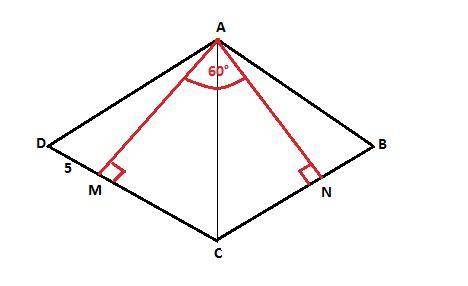
Прямоугольные треугольники DAM и BAN равны по гипотенузе и острому углу (гипотенузы DA и АВ - стороны ромба, ∠D = ∠B как противоположные углы ромба). Следовательно, ∠DAM = ∠BAN, а так как диагональ АС ромба делит ∠DAB пополам (свойство), то ∠MAC = <NAC = 30°. Тогда в прямоугольных треугольниках MAC и NAC ∠АСМ = ∠ACN = 60° (по сумме острых углов прямоугольного треугольника). Тогда угол ∠С ромба равен 120°, а ∠D = 60° (по сумме углов ромба, прилегающих к одной стороне).
В прямоугольном треугольнике DAM ∠ADM = 60°, ∠DAM=30°.
Против угла 30° лежит катет DM = 5 дм. Тогда гипотенуза DA (сторона ромба) равна 10 дм, а периметр ромба равен
10·4 = 40 дм.
Прямоугольник АВСД - основание параллелепипеда, прямоугольник со сторонами 9 и 12 см. АС и ВД - диагонали.
Треугольник ВАС - прямоугольный (по условию), АС - гипотенуза.
АС2=АВ2+ВС2, АС2=81+144=225, АС=15 см.
Треугольник АСС1 - прямоугольный, так как СС1 - высота параллелепипеда.
АС1 - гипотенуза, АС, СС1 - катеты, угол САС1=45 град - значит треугольник АСС1 - равнобедренный, по этому АС=СС1=15 см.
Площадь бок. поверхности= периметр основания*высота
Пл.= (АВ+ВС)*2*СС1 Пл.= (9+12)*2*15=630 см2
ответ: 15 см - высота параллелепипеда, 630 см2 - площадь боковой поверхности параллелепипеда.