Плоскости α и β параллельны. Через точку M, находящуюся между этими плоскостями, проведены две прямые. Одна из них пересекает плоскости α и β в точках A₁ и B₁, а другая — в точках A₂ и B₂ соответственно . Найдите отрезок A₁A₂, если он на 1 см меньше отрезка B₁B₂, MA₂ = 4 см, A₂B₂ = 10 см.
Объяснение:
1) Две пересекающиеся прямые А₁В₁ и А₂В₂ определяют плоскость
(А₁А₂ В₂) единственным образом ( аксиома). Эта плоскость пересекает параллельные плоскости α и β по параллельным прямым А₁А₂ и В₁В₂( свойство).
2) ΔМА₁А₂~ΔMB₁B₂ по 2-м углам : ∠А₁МА₂=∠B₁МB₂ как вертикальные , ∠А₁А₂М =∠В₁В₂М как накрест лежащие при А₁А₂ || В₁В₂, А₂В₂-секущая. Поэтому сходственные стороны пропорциональны
А₁А₂ : В₁В₂ = АМА₂ : МВ₂
А₁А₂ : (А₁А₂+1) = 4: ( 10-4)
4(А₁А₂+1)=А₁А₂*6 ⇒ А₁А₂= 2 cм

ответ: 20 см
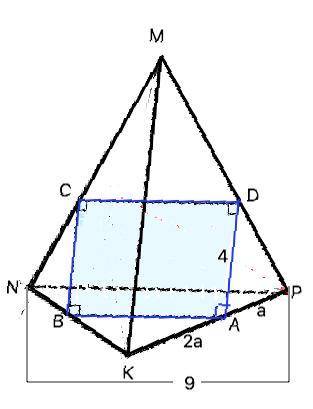
Объяснение: Рассмотрим основание NPK данного тетраэдра. Сторона АВ получившегося прямоугольника параллельна стороне PN треугольника NPK. Треугольники КВА и КNP подобны по двум углам: угол К общий, углы КАВ и КРN равны как соответственные при пересечении параллельных АВ и PN секущей КР.
Из данного в условии отношения отрезков ребра РК примем РА=а, АК=2а, ⇒ РК=РА+АК=а+2а=3а. Коэффициент подобия РК:АК=3:2 . ⇒ PN:АВ=3:2, откуда АВ=2/3 PN=9•2/3=6 дм.
Противоположные стороны прямоугольника равны. Р(АВСD)=2•(АВ+АD)=2•(6+4)=20 (см)
Найти:
Решение:
1) С прямоугольного треугольника АВК(∠АКВ = 90°).
Косинус угла это отношение прилежащего катета к гипотенузе, тоесть:
2) С прямоугольного треугольника CDL (∠CLD = 90°)
Котангенс угла - это отношение прилежащего катета к противолежащему катету, тоесть:
3) основание АD
4)
5) Периметр и площадь трапеции
ответ: