48/2=24 это a+b а и ь стороны,т.к. P=(a+b)*2
24/4=6 т.к. всего частей 4
и получается что 1 часть равна 6*1=6,а вторая 6*3=18
ответ: 6,6,18,18
Якщо ще актуально)
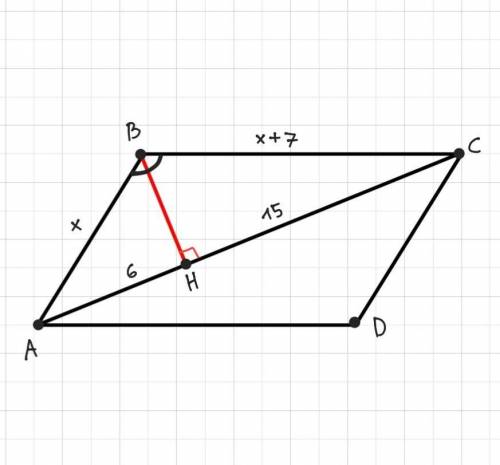
Дано: ABCD - паралелограм, АС - діагональ, ВН⟂АС, АН= 6 см, СН= 15 см, ВС–АВ= 7 см.
Знайти: S abcd.
Розв'язання.
Розглянемо трикутники АНВ і СНВ.
Вони прямокутні, а сторона ВН для них є спільним катетом. АН= 6 см, СН= 15 см, тому очевидно, що ВС>АВ.
Нехай АВ= х см, тоді ВС= (х+7) см.
Оскільки ВН - спільна сторона, тоді справедлива така рівність (через т.Піфагора у ΔAHB і ΔCHB):
АВ²–АН²= ВС²–НС²;
х²–6²= (х+7)²–15²;
х²–6²= х²+14х+49–225;
х²–х²–14х= 36+49–225;
–14х= –140;
14х= 140;
х= 10 (см)
Отже, АВ= 10 см, тоді:
ВН²= х²–6²= 10²–6²= 100–36= 64;
ВН= 8 см (–8 не може бути)
Розглянемо ΔABC:
AC= AH+HC= 6+15= 21 см
ВН= 8 см, ВН - висота ΔABC, оскільки ВН⟂АС.
Знайдемо площу ΔАВС:
S= ½•AC•BH;
S= ½•21•8= 84 (см²).
Діагоналі паралелограма ділять його на два рівних трикутники, тобто їх площі рівні.
SΔABC= SΔCDA= 84 см²
Звідси площа паралелограма ABCD дорівнює
S abcd= 2•SΔABC= 2•84= 168 (см²).
Відповідь: 168 см².
Задача: Знайти радіус кола, вписаного в рівносторонній трикутник, якщо радіус кола, описаного навколо цього трикутника, дорівнює 16 см.
Рішення:
Формула кола, вписаного в рівносторонній трикутник:
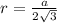, де а — сторона правильного тр-ка
Знайдемо сторону а через формула кола, описаного навколо рівностороннього тр-ка:
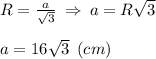
Підставимо значення у формулу кола, вписаного в рівносторонній тр-к
Відповідь: Радіус кола, вписаного в рівносторонній трикутник, рівний 8 см.
Задача: Точка перетину висот BK і PH трикутника BEP є центром вписаного в нього кола. Доведіть, що тр-к BEP рівносторонній.
Рішення:
Центром вписаного в коло трикутника є перетин бісектриса тр-ка, отже і BK та PH є бісектрисами. Висота є бісектрисою, якщо суміжні сторони рівні.
BK — висота/бісектриса ⇒ PB = EB;
PH — висота/бісектриса ⇒ PB = EP.
Відповідно, PB = EB = EP ⇒ ΔBEP — рівносторонній, що і потрібно було довести.
т.к 1:3 то на 2 сторона 4 части значи т на весть периметр 8
48/8=6
1 сторона = 6 вторая 6*3=18 см
ответ 6 6 18 18