Question

Основание пирамиды- квадрат со с тороной 6 в корне2. косинус угла наклона каждого бокового ребра к плоскости онования равен 3/5, найдите объем пирамиды.

Answer 1

Основание пирамиды-квадрат, следовательно

диагональ квадрата d равна 6sart{2}*sqrt{2}=6*2=12.

Половина диагонали равна 12:2=6

Высоту пирамиды h находим из соотношения: cosa=6/h

                                                                      3/5=6/h

                                                                       h=10

S(осн) = 1/2*(d^2)=1/2 *(12^2)=72

V=1/3*S(осн)*h=1/3*72*10=240

Answer 2

1. Находим радиус описанной окружности по формуле:

$R=\frac{a}{\sqrt{2}}$

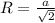
R=6

2. Находим ребро b пирамиды по определению косинуса:

cosα= R/b, b=R/cosα=6/(3/5)=10

3. Находим высоту пирамиды по теореме Пифагора:

b²=h²+R², h=√b²-R²=√100-36=8

4. Находим площадь основания:

S=a²,

S=72

5. Находим объём пирамиды:

V=1/3·S·h

V=1/3·72·8=192(куб.ед.)

ответ: 192 куб.ед.