а). Точка, симметричная данной относительно оси 0Х, лежит на прямой, проходящей через эту точку перпендикулярно оси 0Х, на расстоянии, равном расстоянию от данной точки до оси 0Х. То есть это точка В(-1,5;-2).
б). Точка, симметричная данной относительно оси 0Y, лежит на прямой, проходящей через эту точку перпендикулярно оси 0Y, перпендикулярно оси 0Y, на расстоянии, равном расстоянию от данной точки до оси 0Y. То есть это точка С(1,5;2).
в). Точка, симметричная данной относительно начала координат, лежит на прямой, проходящей через данную точку и начало координат, на расстоянии, равном расстоянию от данной точки до начала координат.
То есть это точка D(1,5;-2).
11
Объяснение:
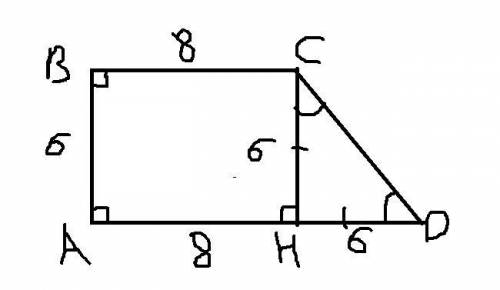
1) Проведём высоту CH на сторону AD.
Рассмотрим прямоугольный треугольник CHD:
∠H = 90° (CH - высота)
∠D = 45° (по условию)
Значит, ∠HCD = 45° и ΔCHD - равнобедренный (2 равных угла C и D); CH, HD - боковые стороны ⇒ CH = HD
2) ∠AHC = 90° (CH - высота)
∠A = ∠B = 90° (условие)
Значит, ABCH - прямоугольник ⇒ CH = AB = 6 (AB = 6 по условию), BC = AH
HD = CH (п.1), HD = 6
3) AD = AH + HD
14 = AH + 6 ⇒ AH = 8
BC = AH (п.2); BC = 8
4) Итак, основания трапеции ВС и AD равны соответственно 8 и 14
Длина средней линии L равна полусумме оснований.
L = (BC + AD)/2 = (8+14)/2 = 11
Площадь трапеции равна произведению полусуммы оснований на высоту
a) В ΔBDE (DE - перпендикуляр к BC) и ΔBHB (BH - перпендикуляр к AD)
BD - общая
BH = DE (условие)
Угол DEB в ΔBDE и угол BHD в ΔDHB равны по 90°, значит по теореме пифагора BE^2 = BD^2 - DE^2
и DH^2 = BD^2 - BH^2
BH = DE
DH^2 = BD^2 - BH^2
BE^2 = BD^2 - BH^2
DH = BE
След - но, ΔBHD = ΔDEB (по трём сторонам)
Значит, угол BDA = угол DBC
BD - секущая, значит BC ll AD
След-но ABCD - трапеция
1-ое основание - AD = 3 см, 2-ое основание - BC = 4 см, высота BH = 2 см
S(ABCD) = (AD + BC) × BH/2 = 7 × 2/2 =
ответ : 7 см^2
b) В ΔBDE (DE - перпендикуляр к BC) и ΔDBH (BH - перпендикуляр к AD)
BD - общая
BH = DE (условие)
Угол DEB в ΔBDE и угол BHD в ΔDBH равны по 90°, значит по теореме пифагора BE^2 = BD^2 - DE^2
и DH^2 = BD^2 - BH^2
BH = DE
DH^2 = BD^2 - BH^2
BE^2 = BD^2 - BH^2
DH = BE
След - но, ΔBHD = ΔDEB (по трём сторонам)
Значит, угол BDA = угол DBC
BD - секущая, значит BC ll AD
След-но ABCD - трапеция
1-ое основание - AD = 5 дм, 2-ое основание - BC = 1,5 дм, высота BH = 2 дм
S(ABCD) = (AD + BC) × BH/2 = 6,5 × 2/2 = 6,5 дм^2 (650 см^2)
ответ : 6,5 дм^2 (650 см^2)