Найдите длину окружности , описанной около:
1)прямоугольника, меньшая сторона которого равна 8 см, а угол между диагоналями равен α;
2)правильного треугольника, площадь которого равна 48√3 см²
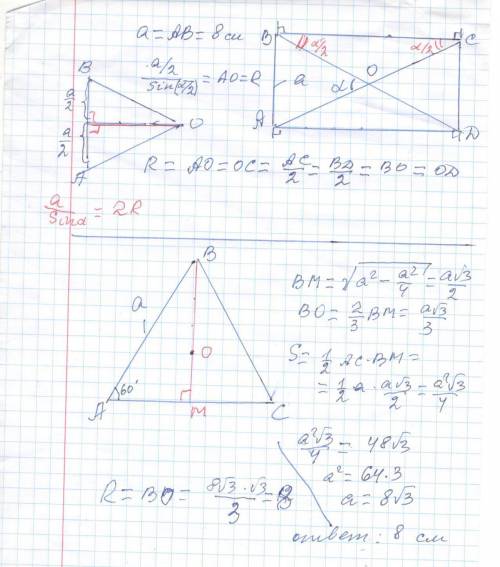
1) R = AC/2 * * * R =d/2 = AC/2 =AO * * *
Из ΔABC: AC =2*AO =AB /sin(α/2) =8/sin(α/2)
R = 4/sin(α/2)
2) a/sinα =2R ⇒ R = a/2sinα =a/2sin60° =a/(2*√3 /2) = a /√3 || (a√3)/3 ||
* * * S = (1/2)*absinC * * * S = (1/2)*a*a*sin60° =(a²√3) / 4
48√3 =(a²√3) / 4 ⇔a²/ 4 = 48 ⇔a² =4*48 = 4*16*3 ⇒ a=8√3
R = a /√3 = 8√3/√3 =8
1. ΔBDC, вписанный в окружность можно представить как <BDC что опирается на хорду ВС.
В ΔСАВ <САВ тоже опирается на отрезок ВС, причем <САВ=<BDC по условию. По теореме о вписанных углах в окружность равные углы опираются на одну и ту же хорду. Значит ΔСАВ вписан в туже окружность с площадью S=25π/4.
Определим радиус:
S=π·r² ⇒ r=√S/π
r=√25π/4π=5/2=2.5
2. Рассмотрим чет. ABCD. Все четыре точки лежат на одной окружности, значит четырехугольник вписан в данную окружность.
Вписать можно только тот выпуклый четырехугольник у которого сумма противоположных углов равна 180°. То есть
<BAD+<BCD=180° <BCD=180°-90°=90°
Выпуклый четырехугольник с двумя противоположными прямыми углами являевся прямоугольником.
S=a·b=3·√16-9=3√7(кв.ед.)