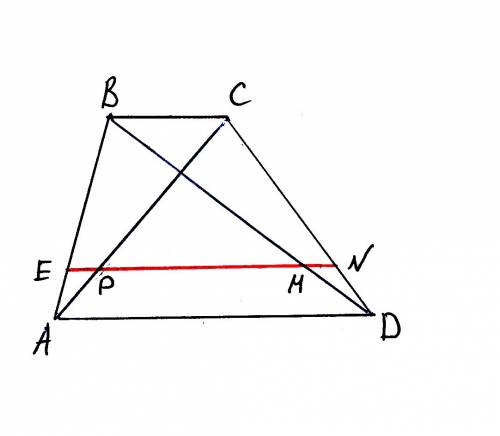
Если прямая проходит ниже точки пересечения диагоналей, то крайние из них являются отрезками, пропорциональными малому основанию. При этом коэффициент пропорциональности определяется расстоянием прямой от большого основания. см.чертеж
Если эта прямая (параллельная основаниям) EN делит высоту трапеции, или диагональ, или боковую строну, или любой другой отрезок прямой, концы которого лежат на разных основаниях трапеции, в следующем отношении -
(К примеру) AE/AB = q
то крайние отрезки будут иметь длину
ЕР = MN = q*b,
где b = BC - малое основание.
Все это следует из простого подобия пар треугольников (ABC и AEP) и (DMN и DBC), а так же теоремой о пропорциональности отрезков секущих между параллельными прямыми (из чего следует, что MD/BD = ND/CD = AP/AC = q).
Для прямых, проходящих выше точки пересечения диагоналей, рассматриваются треугольники, у которых основанием является большое основание трапеции. С тем же результатом :)))
Радиусы , проведённые к точкам касания, образуют угол, равный 120 градусов, тогда отрезок ОВ образует с каждым из радиусов угол 60 градусов. Поскольку треугольники ОВС и ОВА прямоугольные, то отрезок ОВ образует с каждым отрезком касательных угол 30 градусов.
В прямоугольном тр-ке катет, лежащий против угла в 30 градусов, равен половине гипотенузы. И наоборот: гипотенуза в два раза больше катета, лежащего против угла в 30 градусов.
В одном из тр-ков (они одинаковые) ОВС или ОВА гипотенузой является отрезок ОВ, а катетом, лежащим против угла в 30 градусов, радиус окружности, равный 16см.
Следовательно, отрезок ОВ - 2 * 16 = 32(см)
2x+5=20
x=7.5
AC=12.5
BC=7.5
2) AC - x, BC - 4x
5x=20
x=4
AC=4
BC=16