ABCD - прямоугольная трапеция, угол A и угол B - прямые, угол C = 150 (очевидно т.к. угол D- острый) BC = 3 CD=4
Проведем CL перпендикулярно AD таким образом что BC=AL=3
Угол DCL = 150-90=60 (т.к угол BCL - прямой)
Рассмотрим треугольник CLD - прямоугольный с прямым углом L
угол D=180 - (60+90)=30
катет в прямоугольном треугольнике лежащий против угла в 30 градусов равен половине гипотенузы следовательно:
CL = 0.5CD=0.5*4=2
LD по теореме пифагора LD=sqrt[16-4]=sqrt12=2sqrt3
AD = AL+LD= 3+2sqrt3
Площадь трапеции S= (0,5 (a+b)) *h
CL = h
значит S= (0,5(3+3+2sqrt3)) *2=6+2sqrt3
Вроде как правильно
Высота боковой грани называется "апофема".
Линейный угол двугранного угла между боковой гранью и основанием - это угол между апофемой и её проекцией на основание. Если рассмотреть все три треугольника, образованных апофемой любой из граней, её проекцией и высотой пирамиды, то все эти прямоугольные треугольники равны - у них есть общий катет (высота пирамиды) и одинаковые противолежащие острые углы. Это означает, что все апофемы равны между собой, а также - что равны все проекции апофем на основание.
Поскольку все проекции апофем равны, то проекция вершины пирамиды РАВНОУДАЛЕНА от сторон треугольника в основании, то есть это - центр вписанной в основание окружности. То есть доказаны оба пункта.
(на самом деле, если взять ЛЮБУЮ пирамиду - с любым числом граней, и потребовать ТОЛЬКО ОДНО - что все боковые грани одинаково наклонены к основанию, то это автоматически означает, что 1. в МНОГОУГОЛЬНИК в основании МОЖНО вписать окружность, и 2. вершина пирамиды проектируется в центр этой окружности. Все, что дополнительно требуется - чтобы многоугольник в основании был выпуклым.)
Остается вычислить радиус вписанной в основание окружности (который, как было показано, и есть - проекция апофемы).
В основании пирамиды лежит равнобедренный треугольник с основанием а и углом при основании α. Поскольку центр вписанной в такой треугольник окружности лежит на пересечении биссектрисы острого угла α и высоты-медианы-биссектрисы угла при вершине, то для радиуса вписанной окружности сразу можно записать соотношение
r = (a/2)*tg(α/2).
Это - ответ. :)
Я там картинку добавил.
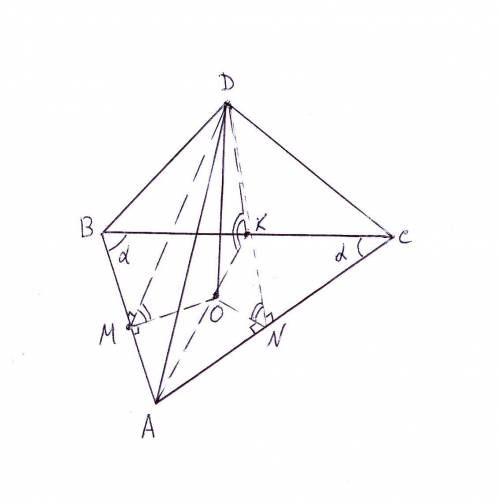
Треугольники DOM, DON и DOK равны. О - проекция вершины D на плоскость АВС, через DO проводится плоскость перпендикулярно АВ, поэтому DM и OM - перпендикуляры к АВ, угол DMO - линейный угол двугранного угла. Треугольники равны, потому что задано, что углы DMO, DKO и DNO равны, а DO - общий катет.
Поэтому О равноудалена от сторон, ОК = r.
Дальше, угол ОСК = α/2, СК = а/2, откуда r = (a/2)*tg(α/2).
AB=1/2AD, AD=2AB
Зная, что сумма острых углов прямоугольного треуг-ка равна 90°, находим угол А:
<A=90-<ADB=90-30=60°
Угол D в трапеции ABCD равен:
<D=30+30=60°
Углы при основании трапеции равны, значит, она равнобедренная, и АВ=CD.
Рассмотрим треугольник BCD. <CBD=<ADB как накрест лежащие углы при пересечении двух параллельных прямых AD и ВС секущей BD. <CDB=30°, значит треугольник BCD равнобедренный, поскольку углы при его основании BD равны.
ВС=CD. Но CD=AB, значит ВС=CD=AB
Таким образом мы можем принять АВ, ВС, CD за х, а AD - за 2х (т.к. AD=2AB см. выше). Зная периметр, запишем:
AB+BC+CD+AD=P
x+x+x+2x=60
5x=60x=12
AD=2*12=24 см
2. Рассмотрим прямоугольный треуг-ик АЕВ. Он равнобедренный по условию (диагональ ВЕ равна стороне АЕ, она будет равна и стороне ВС). В равнобедренном треуг-ке углы при основании равны. Найдем их:
<A=<ABE=(180-<AEB):2=(180-90):2=45°
Поскольку противоположные углы параллелограмма равны, то
<C=<A=45°
<ABC=<AEC=90+<ABE=90+45=135°