ответ: 2688 см²
Объяснение:
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противолежащих сторон равны.
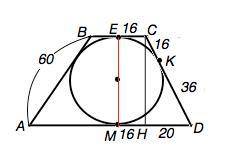
Для трапеции АВСD, в которую вписана окружность, BC+AD=AB+CD=60+16+36=112 см.
Стороны трапеции - касательные к вписанной окружности. Обозначим точки касания на ВС– Е, на СD - К, на AD-М. По свойству равенства отрезков касательных, проведенных из одной точки, СЕ=СК=16, DK=DM=36.
Соединим точки касания на основаниях отрезком ЕМ. Опустим высоту СН. МН=ЕС=16
DH=DM-CE=36-16=20.
По т.Пифагора СН=√(CD²-DH²)=√(52²-20²)=48 (см)
Площадь трапеции равна произведению полусуммы оснований на высоту.
S(ABCD)=0,5(BC+AD)•CH=0,5•112•48=2688 см².
ВАС = 60 гр. АО - биссектриса, О - центр впис. окр-ти. В и С - точки касания.
Пусть точка К прин окр-ти и: КМ перп АС, КМ = 1, KN перп АВ, KN = 4
В прямоугольной трапеции СОКМ: ОС = ОК = r, КМ = 1
Проведем высоту КР на основание ОС. ОР = ОС - КМ = r - 1
Тогда из пр. тр-ка КОР:
КР = кор(ОК^2 - OP^2) = кор(r^2 - (r-1)^2) = кор(2r-1).
КР = СМ = кор(2r-1).
АМ = АС + СМ = rкор3 + кор(2r-1) (т.к. АС = r/tg30 из тр. АОС)
Теперь проведем АК.
Из тр. АКМ : AK = 1/sina, где а - угол КАМ
Из тр. NAK : АК = 4/sin(60-a)
Приравняв, получим:
sin(60-a) / sina = 4, или раскрыв синус разности и поделив почленно:
(кор3)ctga - 1 = 8 ctga = 3кор3
Но из тр-ка АКМ:
ctga = AM/MK = rкор3 + кор(2r-1)
Приравняем и получим:
(3-r)кор3 = кор(2r-1). 1<r<4
3r^2 - 20r + 28 = 0 D = 64 r = 2 (другой корень >4)
ответ: 2