AB == BC => <BAC = <C = (180-120)/2 = 30°.
Зная все углы, и основание равнобёдренного треугольника — формула вычисления боковой стороны такова:
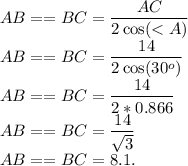
<HBA = 180 - <ABC = 180-120 = 60°
<HAB = 90-60 = 30°.
<AHB = 90°.
Теорема о 30-градусном угле прямоугольного треугольника такова: катет, противолежащий углу 30-градусов — равен половине гипотенузы.
В нашем случае — гипотенуза треугольника AHB — сторона AB, которая равна: 8.1.
Тоесть: HB = AB/2 => HB = 8.1/2 = 4.05.
По теореме Пифагора:
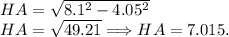
Вывод: HA = 7.015.
Всё решается очень просто.
Если внешний угол треугольника =60 градусов, то внутренний равен 120 градусов.
Теперь дальше. Сумма углов в треугольнике равна 180 градусов, но в равнобедренном треугольнике углы при основании равны, значит они по (180-120)/2=30 градусов.
Я не могу начертить рисунок, но могу дать совет, когда проведёте высоту к боковой стороне, получится прямоугольный треугольник, у которого один угол равен 30 градусов. Основное правило решения задачи:
"Катет лежащий против угла в 30 градусов равен половине гипотенузы"
Надо составить уравнение по теореме Пифагора, и решить.
(Я не знаю правильно ли, но у меня получился ответ 10см)
Вот и всё решение.