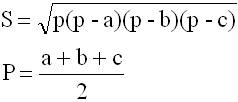Треугольник МКР, МТ=5, КТ=10, МК=15, КР=9, М=12
Периметр = 15+9+12=36, полупериметр=36/2=18
Площадь МКР= корень (18 х (18-15) х (18-9) х (18-12) = корень 2916=54
плошадь МКР = 1/2 х МК х КР х sin угла K
54 = 1/2 х 15 х 9 х sin угла K , sin угла K = 108/135=0,8
МР/ sin угла K = КР / sin угла М, 12 / 0,8 = 9 / sin угла М, sin угла М = 0,8 х 9/12=0,6
площадь треуг КТР = 1/2 х КТ х КР х sin угла K = 1/2 х 10 х 9 х 0,8 =36
площадь МТР = 1/2 х МТ х МР х sin угла М = 1/2 х 5 х 12 х 0,6 =18
Всего 36+18=54
0,13 м = 1,3 дм
0,73 м = 3,7 дм
Дана трапеция ABCD, у которой известны все стороны. Нужно найти высоту, чтобы вычислить площадь.
Проведем отрезок BE к нижнему основанию AD параллельно боковой стороне трапеции CD. Поскольку BE и CD параллельны и проведены между параллельными основаниями трапеции BC и DA, то BCDE - параллелограмм, и его противоположные стороны BE и CD равны. BE=CD.
Рассмотрите треугольник ABE. AE=AD-ED. Основания трапеции BC и AD известны, а в параллелограмме BCDE противолежащие стороны ED и BC равны. ED=BC, значит, AE=AD-BC.
Теперь найдем площадь треугольника ABE по формуле Герона (вложение 2).
p = 4,5
S = 2,4
Найдем высоту
ВО = 2S / AE
BO = 0,6
Высота треугольник является и высотой трапеции.
Sтрап = (2+6)*0,6 / 2 = 2,4 дм .
.