Найдите все углы параллелограмма если разность двух из них равна 1)80 2)120

👇

Увидеть ответ

Ответ:

lexalarionov11

19.03.2022

ответ: 1) 130°; 50° 2) 150°; 30°

Объяснение:

Сумма внутренних углов параллелограмма, прилежащих к одной стороне, равна 180°.

1) Примем больший угол равным х. Тогда меньший равен х=80° => х+х-80°=180° => 2х=260°=>

х=130°.

х-80°=130°-80°=50°

———————

Решение по второму данному аналогично. Больший угол получится равным 150°, меньший - 30°.

Найдите все углы параллелограмма если разность двух из них равна 1)80 2)120

4,7(89 оценок)

Открыть все ответы

Ответ:

alenkaabramovic

19.03.2022

Если воспользоваться готовой формулой для радиуса вписанной в правильный тетраэдр сферы - то всё попроще. но попробуем обойтись без этой формулы.
на первом рисунке изображён тетраэдр и сечение вписанной сферы плоскостью СРТ
Низ красный, верх синий
Примем сторону тетраэдра за 1. тогда в треугольнике АКР
АР = 1/2
∠РАК = 30°
КР/АР = tg(30) = 1/√3
КР = 1/(2√3)
КР/АК = sin(30°)
АК = 2*КР = 1/√3
И так как К - точка пересечения медиан основания, то
СК = АК = 1/√3
Переходим к ΔАРТ
РТ²+АР² = АТ²
РТ² + 1/4 = 1
РТ² = 3/4
РТ = √3/2
Переходим к ΔКРТ
КТ²+1/(2√3)² = (√3/2)²
КТ²+1/(4*3) = 3/4
КТ² = 3/4-1/12 = 9/12-1/12 = 8/12 = 2/3
КТ = √(2/3) - это высота пирамиды
Пора искать радиус вписанной сферы
ΔКРТ и ΔХОТ подобны - общий угол Т, по прямому углу и третий угол равен в силу того, что два равны и сумма углов треугольника 180°
ОХ = ОК = r
КР/ОХ = РТ/ОТ
1/(2√3)/r = √3/2/(√(2/3)-r)
(√(2/3)-r)/(2√3) = √3/2*r
√(2/3)-r = 2√3√3/2*r
√(2/3)-r = 3r
√(2/3) = 4r
r = 1/(2√2√3) = 1/(2√6)
Хорошо :)
В правильный тетраэдр с единичным ребром можно вписать сферу радиуса 1/(2√6)
Если радиус сферы R, то ребро тетраэдра будет a = 1/(1/(2√6)) = 2√6
площадь одной грани
S₁ = 1/2*a²*sin(60°) = 2*6*√3/2 = 6√3
И полна плошадь тетраэдра в 4 раза больше
S = 24√3

Около шара радиуса r описан правильный тетраэдр. найдите площадь поверхности тетраэдра. с рисунком,

Около шара радиуса r описан правильный тетраэдр. найдите площадь поверхности тетраэдра. с рисунком,

4,6(28 оценок)

Ответ:

bobrikov01

19.03.2022

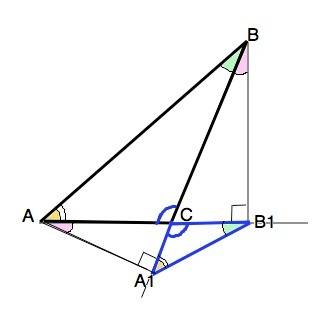
Высоты тупоугольного треугольника, проведенные из вершин острых углов, пересекают прямые, содержащие их стороны, вне треугольника.

Рассмотрим прямоугольные ∆ АСА1 и ∆ ВСВ1.

Острые углы при С у них равны как вертикальные.

Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны. ⇒

∆ АСА1 ~ ∆ ВСВ1

Тогда синусы их равных углов равны, т.е. отношение сходственных катетов к гипотенузам, равно. СА1/ АС=СВ1/ВС

III признак подобия треугольников.

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то такие треугольники подобны. Доказано.