Это очень известная задача, и решается она просто (то есть на уровне школьника) только благодаря подбору данных. Само собой, можно сократить все числа на 100, и искать такую точку К внутри треугольника АВС, что АК + 2*ВК + 3*СК минимально.
Но АК + 2*ВК + 3*СК = АК + СК + 2*(ВК + СК) >= AC + 2*BC.
Всегда. Причем равенство возникает только в случае, если К совпадаетс с С. Во всех других случаях АК + 2*ВК + 3*СК > AC + 2*BC;
Поэтому колодец надо рыть прямо в деревне С.
Если бы в деревне С жило 299 семей, такую задачу с трудом решил бы и профессор, причем настоящий, а не местного разлива :)))
По прежнему не идут вложения. Если нужен подробный рисунок, сообщите эл. адрес. Туда вышлю фотку.
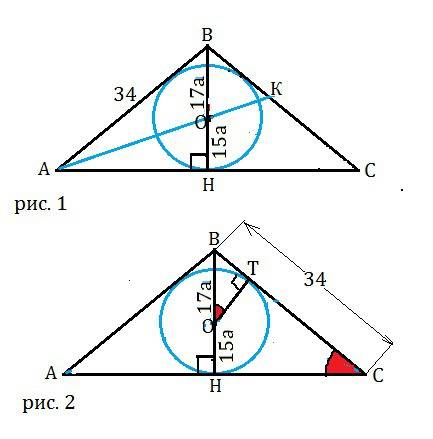
АВС - равнобедр. тр-к. АВ = ВС = х. h = BK - высота, r - радиус вписанной окружности. ОК = r, О - точка пересечения биссектрис - центр вписанной окр-ти. Остальные обозначения и построения - как описаны в условии.
х = ?
Сначала некоторые соотношения через площадь:
S = pr, где р = (х+х+14)/2 = х+7 - полупериметр. S = (x+7)r
S = AC*h/2 = 7h
Приравняв, выразим h через r:
h = (x+7)r/7. (1)
Из тр.АОК: tgA/2 = r/7
Из тр. АВК: tgA = h/7
Из тригонометрии: tgA = 2tgA/2 / (1-tg^2(A/2)) = 14r/(49-r^2)
Значит h = 7tgA = 98r/(49-r^2) (2)
Приравняв (1) и (2), получим выражение для х через r:
х = (686/(49-r^2)) - 7 = (343+7r^2)/(49-r^2) (3)
Задача сводится к нахождению r^2.
Треугольники AMN и АВК - подобны (мы провели MN перпенд. АС)
АМ/АВ = MN/ВК = AN/АК = 7/8 (следует из условия МВ = АВ/8)
Значит: MN=7h/8 = 343r/(4(49-r^2)),
AN = 7AK/8 = 49/8, ND = AD - AN = 28 -(49/8) = 175/8
Из пр. тр-ка DOK: tgD/2 = r/KD = r/21
Из пр. тр. DMN: tgD = MN/ND = 686r/(175(49-r^2)) (4)
Через тригонометрию:
tgD = 2tgD/2 /(1-tg^2(D/2)) = 42r/(441-r^2) (5)
Приравняв (4) и (5), получим уравнение для r^2:
686r/(175(49-r^2)) = 42r/(441-r^2)
7/(25(49-r^2)) = 3/(441-r^2)
r^2 = 588/68 = 147/17 (6)
Теперь подставим (6) в (3) и найдем боковую сторону:
ответ: 10