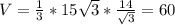Дана равнобедренная трапеция АВСД. АВ и СД - боковые стороны. ВС - меньшее основание. По условию (и св-вам равнобедренной трапеции) АВ=СД=ВС
Проведем диагональ ВД. По условию угол АВД=120 градусов.
Проведем вторую диагоняль СА. (точка их пересечения О)Треугольник ВСО равнобедренный (по свойствам равн. трапеции), где ВО=ОС и угол ОВС=углу ВСО = х.
Треугольник АВС тоже равнобедренный. У него АВ=ВС (по условию) => Угол ВАС=углу ВСА(или ВСО) => угол АВС=углу ВСО=углу ОВС = х.
Найдем чему равен х:
120+х это угол АВС
120+х+х+х=180
3х=60
х=20 градусов.
Следовательн, углы при меньшем основании = 120+20=140 градусов (каждый по 140)
Углы при большем основании = (360-140-140):2=40 градусов (каждый по 40)
V=60 см³
Объяснение:
1.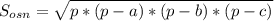
a=6 см, b=10 см, c=14 см
2. по условию известно, что каждое боковое ребро наклонено к плоскости основания под углом 45°, => высота пирамиды проектируется в центр описанной около треугольника окружности.
радиус описанной около треугольника окружности:
3. рассмотрим прямоугольный треугольник:
катет r=14/√3 см - радиус описанной окружности
катет Н =r=14/√3 см (каждое боковое ребро наклонено к плоскости основания под углом 45°)
4.