Объяснение:
D=2R=12см
α=90°
V- ?
радиус основания конуса
R=D/2=12/2=6 см
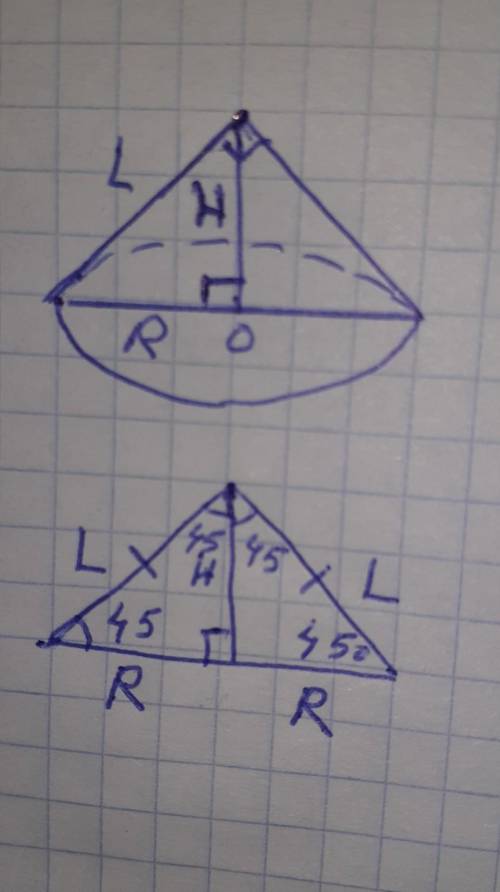
угол при вершине осевого сечения α=90° , то есть прямой угол. значит образующая конуса наклонена под углом 45° к плоскости основания и сечение выглядит как равнобедренный прямоугольный треугольник.
высота конуса равна радиусу основания конуса ,H=R=6см
так как вершина конуса перпендикулярно основанию конуса, и угол при вершине между высотой и образующей конуса 180°-90°-45°=45°
объем конуса
V=1/3 ×πR²×H=1/3 ×π×6²×6=72π см³
или V=72π=72×3,14=226,08 см³
Объяснение:
D=2R=12см
α=90°
V- ?
радиус основания конуса
R=D/2=12/2=6 см
угол при вершине осевого сечения α=90° , то есть прямой угол. значит образующая конуса наклонена под углом 45° к плоскости основания и сечение выглядит как равнобедренный прямоугольный треугольник.
высота конуса равна радиусу основания конуса ,H=R=6см
так как вершина конуса перпендикулярно основанию конуса, и угол при вершине между высотой и образующей конуса 180°-90°-45°=45°
объем конуса
V=1/3 ×πR²×H=1/3 ×π×6²×6=72π см³
или V=72π=72×3,14=226,08 см³

Я подскажу идею, а вы решите ее. Нужно параллельно перенести одну из диагоналей (для определенности BD) на вектор BC. Тогда получившийся треугольник
ACK(K - точка пересечение перенесенной диагонали с прямой AD) равнобедренный( так как у равнобедренной трапеции диагонали равны). Но ее высота равна высоте трапеции. А по условию высота равна средней линии. Но так как мы перенесли диагональ BD на вектор BC то основание AK треугольника равна сумме оснований, значит равна 2 средних линий= 2 высот этого же треугольника. Знач-ит треугольник прямоугольный. угол ACK=90. А значит диагонали перпендикулярны.
P.S. Если остались какие-то вопросы, напишите.