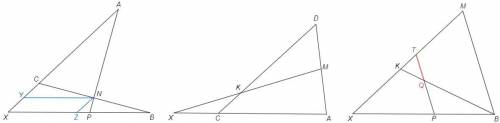
Построим сечение плоскостью через точки PMB
X - пересечение BP и AC
K - пересечение XM и DC
KMB - сечение
PT||BM, QT - искомый отрезок
В плоскости ABC:
проведем NY||BX
CY/YX =CN/NB =1
AY/YX =AN/NP =6/1
CY=YX=x, AY=6x, AC=5x => AC/CX =5/2
проведем NZ||AX
XZ/ZB =CN/NB =1
XZ/ZP =AN/NP =6/1
XZ=ZB=6x, ZP=x, PB=5x => XP/PB =7/5
В плоскости ADC:
AC/CX *XK/KM *MD/DA =1 (т Менелая) => 5/2 *XK/KM *1/2 =1 => XK/KM =4/5
В плоскости сечения KMB:
XT/TM =XP/PB =7/5 => TM/XM =5/12
XK/KM =4/5 => KM/XM =5/9
TM/KM =5/12 *9/5 =3/4 => KT/TM =1/4
QT/BM =KT/KM =1/4 => QT =1/4 a

Объяснение:
№1 фото
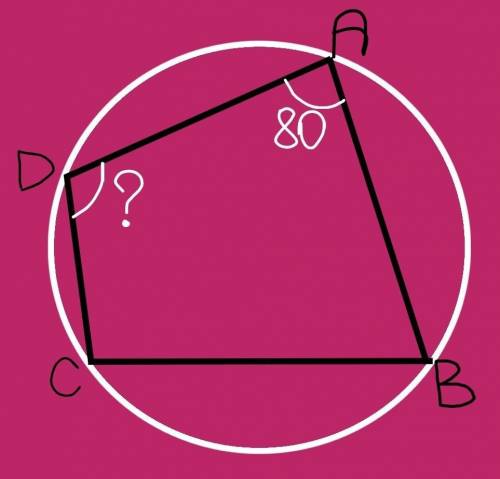
Условие некорректно! Скорее всего надо было найти угол С.
Около четырехугольника можно описать окружность, если сумма его противоположных углов равна 180°.
Углу А противоположен угол С, тогда угол С=180°–угол А=180°–80°=100°.
ответ: б) 100°
Найти угол D, незная угол В или не имея других данных, невозможно.
№2
Около четырехугольника можно описать окружность, если сумма его противоположных углов равна 180°.
Тогда угол CDA=180°–угол АВС=180°–110°=70°.
Сумма углов в любом треугольнике равна 180°.
Следовательно угол ACD=180°–угол CAD–угол CDA=180°–50°–70°=60°
ответ: в) 60°
№3
В четырехугольник можно вписать окружность, если суммы его противоположных сторон равны.
Тоесть ВС+AD=AB+CD
Пусть АВ=4n, тогда CD=3n.
Подставим значения в уравнение:
13+22=4n+3n
35=7n
n=5
Тогда CD=3*5=15 см
ответ: а) 15 см.
1. Проведем АО1 - искомое расстояние. Проведем ОО1 - высоту призмы.
ОО1 = 1, Стороны оснований призмы равны : а = 4.
АО - половина диагонали основания и равна (акор2)/2 = 2кор2.
Из пр. тр-ка АО1О найдем АО1 по теореме Пифагора:
АО1 = кор(1+8) = 3
ответ: 3.
2. Построим тр-ик АС1В. Он равнобедренный АС1 = ВС1 = кор(1+1) = кор2
АВ = 1. Проведем высоты С1К на основание АВ и искомую высоту АМ на боковую сторону ВС1. Пусть С1К = H, AM = h = ?
Найдем сначала H:
Из пр.тр. АС1К: H = кор(2-(1/4)) = (кор7)/2
Тогда площадь АВС1: S = (1/2)*1*(кор7)/2 = (кор7)/4
С другой стороны: S= (1/2)*(кор2)*h
Приравняв, получим: h= (кор7)/(2кор2) = (кор14)/4
ответ: (кор14)/4
3.
а) Строим тр-ик АВ1Д1. Он равносторонний, его стороны - диагонали граней куба и они равны кор2.
Искомое расстояние - высота этого равностороннего тр-ка.
h = (кор2)*(кор3)/2 = (кор6)/2.
ответ: (кор6)/2.
б) Строим тр-ик АА1С. Он прямоугольный. Катеты АА1 = 1 и АС = кор2.
Гипотенуза - диагональ куба А1С = кор(1+1+1) = кор3
В задаче надо найти высоту, опущенную на гипотенузу:
h = ab/c = (кор2)/(кор3) = (кор6)/3.
ответ: (кор6)/3
в) это расстояние до другой диагонали куба. Оно точно такое же, как в п.б)
ответ: (кор6)/3