Дано:
ΔABC - прямоугольный (∠A = 90°)
AB = 14
AE = 4
EB = 10
ED = 6
(•) D - середина гипотенузы (BC)
Найти:
AC
• Пусть половина гипотенузы (BC) = x, т.е.:
CD = DB = x
• Рассмотрим ΔEDB, по теореме косинусов:
ED² = EB² + DB² - 2 • EB • DB • cos∠CBD
( cos∠CBD = AB/CB = 14/2x )
6² = 10² + x² - 2 • 10 • x • 14/2x
36 = 100 + x² - 20x • 14/2x
36 = 100 + x² - 140
x² - 76 = 0
x² = 76
x = √76
x = √(4 • 19)
x = 2√19
• Находим гипотенузу:
BC = 2 • x = 2 • 2√19 = 4√19
• В прямоугольном треугольнике ABC по теореме Пифагора:
BC² = AB² + AC², ⇒ AC = √(BC² - AB²)
AC = √((4√19)² - 14²) = √(304 - 196) = √108 = 6√3
ответ: AC = 6√3
1) AB = 17
2) S = 60
3) ∠AED = 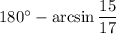
∠EDA = 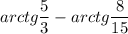
Объяснение:
По свойству биссектрисы 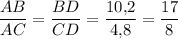
Пусть AB = 17x, AC = 8x. Тогда периметр треугольника 40 = 10,2 + 4,8 + 17х + 8х = 15 + 25х ⇒ х = 1 ⇒ AB = 17, AC = 8; BC = 10,2 + 4,8 = 15.
Заметим, что AC² + BC² = 8² + 15² = 289 = 17² = AB², то есть треугольник прямоугольный с прямым углом C по теореме, обратной теореме Пифагора. Его площадь 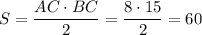 .
.
∠AED = 180° - ∠CED = 180° - ∠A = 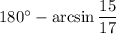
Треугольники ABC и EDC подобны по двум углам (∠C — общий, ∠A = ∠E по параллельности AB и DE). 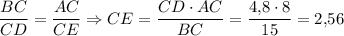
∠EDA = ∠CDA - ∠CDE = 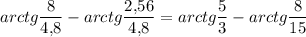
стороны/ребра основания а=1 b=2
высота/ребро c=3
КВАДРАТЫ диагоналей основания параллелепипеда
d1^2=a^2+b^2-2*a*b*cos60 =1^2+2^2-2*1*2*cos60=3
d2^2= a^2+b^2-2*a*b*cos120 =1^2+2^2-2*1*2*cos120=7
диагонали параллелепипеда
D1=√(d1^2+c^2) = √(3+3^2)= √12=2√3
D2=√(d2^2+c^2) = √(7+3^2)= √16=4
ответ 2√3 ; 4