А1С1 – диагональ квадрата со стороной, равной 6 см
Формула диагонали квадрата d=a√2 ⇒
A1C1=6√2
B1D1=A1C1=6√2
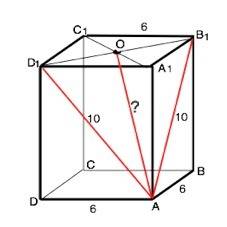
Проведем в боковых гранях диагонали AD1 и АВ1
Боковые ребра параллелепипеда равны, основание – квадрат по условию ⇒
треугольник В1АD1 равнобедренный, т.к. диагонали равных граней равны. Диагонали квадрата равны и точкой пересечения делятся пополам. OB1=OD1=3√2
О - центр А1С1. ⇒
АО - медиана ∆ D1AB1. По т.Пифагора из треугольника АОВ1 найдем длину искомого отрезка
АО=√(AB1*-ОВ1*)=√(100-18)=√82
Если на одной из двух прямых отложить последовательно равные отрезки и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Обобщенная теорема Фалеса:
отрезки, высекаемые параллельными прямыми на одной прямой, пропорциональны отрезкам на другой прямой.
Рассмотрим рисунок, данный во вложении.
Согласно теореме
2:3=7:х
2х=21
х=10,5 см
Обратим внимание на то, что сумма двух отрезков на стороне а равна длине третьего отрезка.
Т.е. 2+3=5.
Согласно т.Фалеса
у=7+х
у=7+10,5=17,5 см
К тому же результату придём, если составим и решим пропорцию
3:5=10,5:у
у=52,5:3=17,5
----------
Добавлю, что задачу можно решить через подобие треугольников отношением их сторон. Только это несколько длиннее.