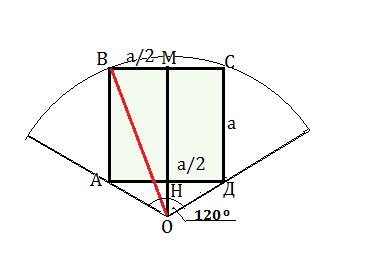
В сектор, центральный угол которого 120 градусов, вписан квадрат со стороной а. Найти радиус сектора.
Обозначим вписанный квадрат АВСД,
В и С - точки касания с дугой сектора, точки А и Д - с его сторонами-радиусами, О - вершина угла сектора.
∆ АОД - равнобедренный, углы при А и Д равны 30º.
Из О проведем биссектрису угла АОД до пересечения с ВС в точке М. Обозначим точку пересечения с АД - Н.
Тогда ВО - искомый радиус R
R²=МО²+МВ²
МВ=а/2
МО=МН+НО
МН=а,
ОН=ДН*tg30º=(а/2)*1/√3=a/2√3
МО=а+a/2√3=а(2√3+1)
R²=[3a²+a²(2√3+1)²]:12
R²=a²(4+√3):3
R=a√(4+√3):√3
--------------------------------------------------
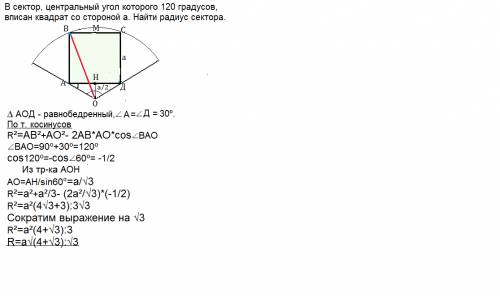
Или по т. косинусов:
R²=АВ²+АО²- 2АВ*АО*cos∠ВАО
∠ВАО=90º+30º=120º
cos120º=-cos∠60º= -1/2
Из ∆ АОН
АО=АН/sin60º=a/√3
R²=а²+а²/3- (2а²/√3)*(-1/2)
R²=а²(4√3+3):3√3=а²(4√3+√3*√3):3√3
Сократим выражение на √3
R²=а²(4+√3):3
R=a√(4+√3):√3
О - точка пересечения высот.
Диагонали ромба взаимно перпендикулярны.
Так как высоты треугольника пересекаются в одной точке, а в равнобедренном треугольнике ABD АМ - высота, то точка О лежит на АМ.
ΔDKB = ΔBHD по гипотенузе и катету (BD - общая гипотенуза, ВН = DK), значит ОВ = OD.
Тогда ОК : OD = ОК : ОВ = 1 : 2.
В прямоугольном треугольнике КОВ катет равен половине гипотенузы, значит ∠КВО = 30°.
ΔАВН: ∠АНВ = 90°, ⇒ ∠ВАН = 60°.
∠BAD = ∠BCD = 60°
∠ABC = ∠ADC = 180° - 60° = 120° так как сумма углов параллелограмма, прилежащих к одной стороне, равна 180°