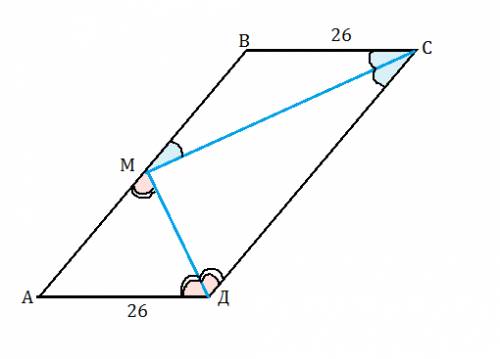
1. Обазанчим пар-мм: ABCD, начиная с нижнего левого угла, точка М - точка пересечения биссектрис, M лежит на АВ
2. Углы ВСМ и МСD равны, т.к. СМ - биссектриса угла С, углы ADM и MDC равны, т.к. DM - биссектриса угла D
3. Приме за меньшую сторону ВС=AD=26 (т.к. противолежащие стороны в пар-мме равны и параллельны)
4. угол MCD=углу CMB как накрест лежащие, при пересечении параллельных прямых CD и АВ секущей МС ⇒ ΔМВС - равнобедренный, ВС=ВМ=26
5. угол МDC=углу DMA как накрест лежащие, при пересчении прямых параллельных CD и AB секущей MD ⇒ ΔMAD - раавнобедренный, AD=AM=26
6. АВ=CD - большая сторона, AB=BM+AM=26+26=52
ответ: большая сторона = 52
По свойству медиан точка их пересечения О делит их в отношении 2:1, считая от вершины (свойство).
Медиана из D пересекает ВС в т.Е. ВЕ=СЕ, ⇒ АЕ медиана ∆ АВС.
МО лежит в плоскости АЕD, которая пересекается с плоскостью АВС по прямой АЕ.
В ∆ АЕD точка М - середина АD, АМ=DМ, ЕО=0,5 DО, следовательно, прямые АЕ и МО не параллельны и пересекутся вне плоскости ∆ ВСD в некоторой точке К, принадлежащей плоскости АВС и лежащей на продолжении медины АЕ.