Объяснение:
Сумма острых углов в прямоугольном треугольнике равна 90°
1) <B=90°-<А=90°-36°=54°
ответ: <В=54°
2) Сумма острых углов в прямоугольном треугольнике равна 180°
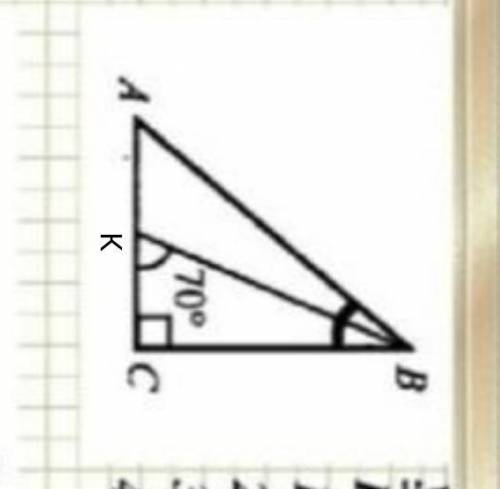
<СВК=90°-70°=20°
ВК- биссектрисса
<СВА=2*<СВК=2*40°=80°
Сумма острых углов в прямоугольном треугольнике равна 90°
<САВ=90°-<СВА=90°-80°=10°
ответ: <САВ=10°
3) ВС- катет против угла 30°
ВС=1/2*АВ=15/2=7,5см
ответ: ВС=7,5см
4)
Катет ВС равен половине гипотенузы АС. В том случае когда лежит против угла 30°
Угол <А=30°.
Сумма острых углов в прямоугольном треугольнике равна 90°
<С=90°-30°=60°
ответ: <А=30°; <С=60°
Билет 1.
1. Точка и прямая - основные фигуры на плоскости. Они не имеют определения. Точка не имеет размеров (длины, ширины, радиуса). Точки обозначаются заглавными латинскими буквами.
Прямая бесконечна. Ее можно представить как туго натянутую нить, бесконечную в обе стороны. На рисунке изображается часть прямой. Прямая обозначается по названию двух точек, лежащих на ней, или строчной латинской буквой.
Отрезок - это часть прямой, ограниченная точками с двух сторон. Точки, ограничивающие отрезок, называются его концами. Отрезок имеет длину. Отрезок обозначается двумя заглавными латинскими буквами - по названию его концов.
2. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство. Построим треугольник А₁В₁С₁, совместив равные стороны АС и А₁С₁ данных треугольников, как на рисунке, так, чтобы вершины В и В₁ оказались по разные стороны от прямой АС.
Тогда ΔВАВ₁ равнобедренный и значит ∠1 = ∠2 как углы при основании равнобедренного треугольника,
ΔВСВ₁ равнобедренный и ∠3 = ∠4, ⇒
∠АВС = ∠АВ₁С и значит ΔАВС = ΔА₁В₁С₁ по двум сторонам и углу между ними.
Билет 2.
1. В зависимости от вида углов треугольники бывают:
остроугольные (все углы острые);прямоугольные (один угол прямой);тупоугольные (один угол тупой);В зависимости от сторон:
разносторонние (нет равных сторон);равнобедренные (две стороны равны);равносторонние (все стороны равны).2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Дано: с∩а, c∩b, ∠1 = ∠2.
Доказать: a║b.
Доказательство:
∠3 = ∠1 как вертикальные,
∠2 = ∠1 по условию, значит
∠3 = ∠2, а эти углы - накрест лежащие при пересечении прямых а и b секущей с, значит а║b по первому признаку параллельности прямых (по накрест лежащи углам).
Гипотенуза АВ=25, катет СВ=20.
Так как высота прямоугольного треугольника делит его на подобные, проекцию катета можно вычислить по т.Пифагора из подобия треугольников.
Для этого сначала находят второй катет.
Но из того же подобия выведено, что:
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу. ⇒
ВС²=АВ•ВН
400=25•ВН, откуда проекция катета ВС на гипотенузу
ВН+400:25=16.