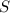 данного сечения =
данного сечения = 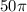 ед.кв.
ед.кв.
Объяснение:
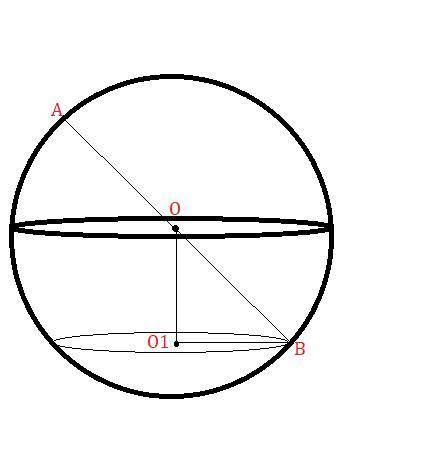
Пусть будет дан шар с центром в точке 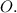
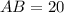 ед.
ед.
Через точку 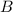 проведём плоскость под углов
проведём плоскость под углов 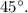
Пусть будет плоскость с центром в точке 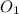 .
.
Тогда 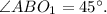
========================================================
Так как 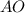 и
и 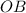 - радиусы данного шара
- радиусы данного шара 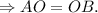
Т.е. 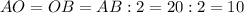 ед.
ед.
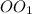
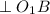 , так как
, так как 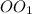 - серединный перпендикуляр.
- серединный перпендикуляр.
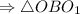 - прямоугольный.
- прямоугольный.
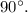
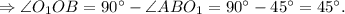
Так как 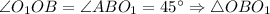 - равнобедренный.
- равнобедренный.
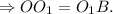
Пусть  -
- 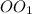 и
и 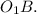
По теореме Пифагора:
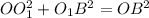
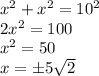
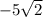 - отрицательное число, поэтому не подходит.
- отрицательное число, поэтому не подходит.
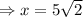
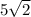 ед. -
ед. - 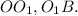
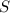 данного сечения =
данного сечения = 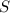 круга =
круга = 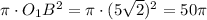 ед.кв.
ед.кв.
Известно, что против равных сторон в треуг-ке лежат равные углы (либо пропорционально большие, если сторона больше)
Так же и здесь
BKC=2KBC значит 2KC=BC
KC=корень6 /2
DK=корень6-корень6/2=корень6 /2
ADK -прямоугольный с гипотенузой АК(лежит напротив прямого угла)
Тогда AK2=AD2+DK2
AK2=(корень6)2+((корень6)/2)2=6+6/4=7,5
AK=корень(7,5)