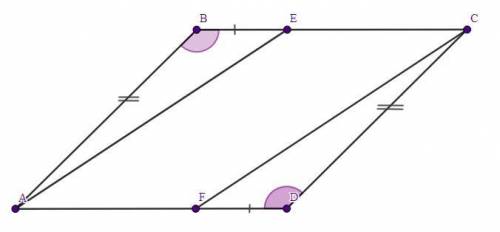
Четырёхугольник ABCD - параллелограмм.
ВЕ = DF (Е ⊂ ВС, F ⊂ AD).
Доказать :Четырёхугольник AECF - параллелограмм.
Доказательство :В параллелограмме противоположные углы и противоположные стороны равны между собой (свойство параллелограмма).Отсюда следует, что ∠В = ∠D, АВ = CD.
Рассмотрим ΔАВЕ и ΔCDF.
ВЕ = DF (по условию)
∠В = ∠D, АВ = CD (по выше сказанному) ⇒ ΔАВЕ = ΔCDF по двум сторонам и углу между ними (первый признак равенства треугольников).
Из равенства треугольников следует и равенство сторон АЕ и CF.
AD = BC (по свойству параллелограмма), но в своё очередь AD = BE + EC ; BC = DF + AF. Учитывая равенство из условия получаем, что ЕС = AF.
Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник - параллелограмм (свойство параллелограмма).АЕ = CF ; ЕС = AF (по выше сказанному) ⇒ четырёхугольник AECF - параллелограмм.
ответ :Что требовалось доказать.
Т.к. угол КLМ =120°, угол МNК=60°
LN - биссектриса.
Углы МLN=КLN=60°
В окружности равные вписанные углы опираются на равные дуги и на равные хорды.
Хорды МN=КN.
Треугольник КNМ - равнобедренный с равными углами при стороне КМ.
Из суммы углов треугольника углы при КМ равны по 60°⇒
треугольник КМN - равносторонний.
По т.косинусов найдем сторону КМ из треугольника КLМ.
КМ²=4²+6²-2*4*6*cos (120°)
KM²=76
Из треугольника МLN по т.косинусов выразим сторону MN
МN²=LМ²+LN²-2*6*LN*cos(60°)
76=36+LN²-6*LN
LN²-6*LN-40=0
Решив квадратное уравнение (вычисления сделаете сами),
LN=10
Второй корень отрицательный и не подходит.