Question

Решите, , . с рисунком и решением. через конец a отрезка ab проведена плоскость альфа. через точку m-середину отрезка ab- и точку b проведены параллельные прямые, пересекающие плоскость альфа в точках m1 и b1 соответственно. а) докажите, что точки a, b1, m1 лежат на одной прямой. б) найдите bb1, если mm1=4 см.

Answer 1

Точки А и М лежат на одной прямой,
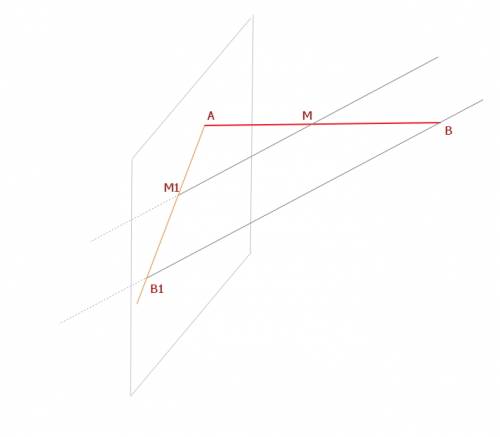
точка М1 по условию лежит в плоскости альфа...
через эти три точки можно провести плоскость (АММ1), которая будет пересекаться с плоскостью альфа, т.к. по условию для этих плоскостей точка М1 --общая...
пересечение двух плоскостей ---это прямая линия)))
точи А и М1 принадлежат по условию и плоскости альфа, и плоскости (АММ1), следовательно эти точки лежат на прямой, которая является пересечением этих плоскостей...
про В1 аналогично... В1 тоже принадлежит плоскости (АММ1)
получили треугольник АВВ1, в нем ММ1 -- средняя линия...
следовательно, ВВ1 = 4*2 = 8

Answer 2

Смотри рисунок к задаче в прикрепленном файле.

1) Так как M1B1 || BB1 значит можно провести плоскость β (по теореме, через параллельные прямые можно провести плоскость, и при том только одну).
М є ММ1, М є АВ => M є β
В є ВВ1, В є АВ => B є β

Следовательно, отрезок АВ будет лежать в β плоскости, потому как уже А и В точки его принадлежат плоскости.
α пересекает β по M1B1, AB є β => A, M1, B1 лежат на общей прямой пересечения плоскостей α и β

2) ΔАММ1 ~ ΔABB1 по 3ему признаку (за 3мя углами). Следовательно, выполняется следующее отношение:
$\frac{AM}{AB} = \frac{MM1}{BB1} \\ \frac{1}{2}= \frac{4}{x} \\ x=8-BB1$