Площадь трапеции равна произведению полусумма оснований на высоту
Номер 1
Прямоугольная трапеция,высота отсекает равнобедренный треугольник,поэтому АК=ВК=8
По условию задачи,АК=КD,следовательно
АD=8•2=16
S=(8+16):2•8=24:2•8=12•8=96 ед.в квадрате
Номер 2
Высота DM отсекла прямоугольный равнобедренный треугольник,где
DM=MA=25-14=11
S=(14+25):2•11=214,5 ед в квадрате
Номер 3
Трапеция равнобедренная по условию задачи
Треугольник АВЕ прямоугольный равнобедренный
АЕ=ВЕ=4
Если опустить высоту из точки С ,то получится точно такой же треугольник и DC1=4
S=(5+13):2•4=36 ед в квадрате
Номер 4
Высота ВМ отсекла прямоугольный треугольник,<А=30 градусов,а значит катет ВМ( он же высота трапеции) равен половине гипотенузы
ВМ=10:2=5
S=(4+15):2•5=19:2•5=9,5•5=47,5 eд в квадрате
Объяснение:
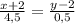, или приведя к целым знаменателям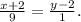 
a,b,c,m,n – вектора
m=a+2b-c,
n=2a-b,
|a|=2,
|b|=3
Ψ = 60⁰ (угол между векторами a и b)
c перпендикулярно a;
c перпендикулярно b.
(mn) – ?
Заметим, т.к. c перпендикулярно a, то их скалярное произведение равно нулю
(ас) = 0. (*)
Аналогично
(bc) = 0. (**)
Умножаем скалярно
(mn) = (a+2b-c)(2a-b)=2|а|²-(ab)+4(ab)-2|b|²-2(ac)+(bc).
С учётом (*) и (**), последние два слагаемых равны нулю (и Ваш неизвестный вектор С пропал!)
(mn) = 2|а|²+3(ab)-2|b|² = 2|а|²+3|a|•|b|cos60⁰-2|b|² =
= 2•2²+3•2•3•0,5-2•3² = -1.
(mn) = -1 – ответ.