а) Нет.
б) Да.
в) Нет.
Объяснение:
Прямая а параллельна прямой l, прямая l - лежит в плоскостях α и β. Значит прямая а
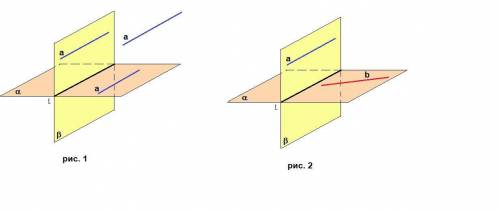
либо лежит в одной из плоскостей (так как параллельные прямые - это прямые, которые лежат в одной плоскости и не пересекаются), либо параллельна этим плоскостям (так как по признаку параллельности прямой и плоскости: если прямая, не лежащая в плоскости, параллельна прямой, лежащей в плоскости, то она параллельна плоскости).Возможные варианты расположения прямой а относительно плоскостей α и β на рисунке 1.
а) Могут ли прямые а и b лежать в одной плоскости?
Нет. По определению, скрещивающиеся прямые - это прямые, не лежащие в одной плоскости.
б) Могут ли прямые а и b лежать в разных плоскостях?
Да. Вариант такого расположения прямых на рисунке 2.
в) Могут ли прямые а и b пересекать плоскости α и β?
Нет, так как прямая а либо лежит в одной из плоскостей, либо параллельна им, т.е. не пересекает.
Пусть D - середина гипотенузы AC, M лежит на AB, N лежит на BC. Поскольку вписанный угол B прямой, он опирается на диаметр. Итак, MN - диаметр этой окружности. По условию AC=2MN, причем AD=DC=BD (медиана прямого угла равна половине гипотенузы). Поэтому BD, будучи хордой этой окружности, равна диаметру. Следовательно, BD также является диаметром. Поэтому диагонали BMDN в точке пересечения делятся пополам, откуда BMDN - параллелограмм, а раз угол B прямой, это прямоугольник. Хотя это уже для нас не важно. Важно то, что MD параллельно BC, откуда MD - средняя линия треугольника ABC, то есть M - середина AB. Точно так же N - середина BC.
а)Через любые три точки можно провести единственную плоскость,значит получается 4 плоскости АBC,ADC,ABD,BDC.
Каждые три точки образуют треугольник(вариант когда 3 точки лкжат на одной прямой не устраивает по условию задачи:точки должны лежать в разных плоскостях)
Рассмотрим треугольники ABC и ADC:
EF и MK являются средними линиями этих треугольников соответственно(по определению).
Значит по свойству средних линий они параллельны стороне AC.
Две прямые,параллельные третьей также параллельны(согласно следствию теоремы о плоскости,проходящей через прямую,параллельную к другой плоскости, и пересекающей данную плоскость)
Значит KM||EF.
Аналогично из треугольников CDB и ADB следует,что KE||MF,значит EFMK-параллелограмм по опредделению.
б)По свойству средней линии треугольника она равна половине параллельной стороны.
Значит KM=EF=3
KE=MF=4
P=KM+EF+KE+MF=14