Угло при нижнем основании равнобедренной трапеции меньше 90°, а при верхнем больше 90°, поэтому ∠A = 60° - угол основания.
Нам неизвестно какая сторона боковая, известно только то, что они смежные. Поэтому решим два варианта.
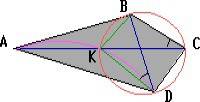
1. AB - нижнее основание.
H₁, H₂ ∈ AB; DH₁ , CH₂ ⊥AB ⇒ DH₁ ║ CH₂
ΔADH₁ = ΔCBH₂ - по гипотенузе и острому углу т.к. трапеция равнобедренная.
AH₁ = H₂B - как соответственные стороны равных Δ.
∠H₂CB = 90° - ∠CBH₂ = 90° - 60° = 30° - как острые улг. в прямоугольном Δ.
H₂B = BC/2 = 20/2=10 - как катет лежащей напротив угла в 30° в прямоугольном Δ.
H₁H₂ = 32 - 10*2 = 12 = т.к. DH₁ ║ CH₂ и DH₁ = CH₂ - как соответственные стороны равных Δ.
P - периметр.
P = AB+ 2BC + CD = 32 + 40 + 12 = 84.
ответ: 84.
2. AB - боковая сторона.
H₁, H₂ ∈ AD; BH₁ , CH₂ ⊥AD ⇒ BH₁ ║ CH₂ ⇒ BH₁ = CH₂ - как параллельные отрезки заключённые между параллельными прямыми, поэтому BCH₂H₁ - прямоугольник ⇒ H₁H₂ = BC = 20.
ΔABH₁ = ΔCDH₂ - по гипотенузе и острому углу т.к. трапеция равнобедренная.
AH₁ = H₂D - как соответственные стороны равных Δ.
∠ABH₁ = 90° - ∠BAH₁ = 90° - 60° = 30° - как острые улг. в прямоугольном Δ.
AH₁ = AB/2 = 32/2=16 - как катет лежащей напротив угла в 30° в прямоугольном Δ.
BC = AD т.к. BH₁ ║ CH₂ и BH₁ = CH₂ - как соответственные стороны равных Δ.
AD = 20 + 16·2 = 52
P - периметр.
P = 2AB + BC + DA = 64 + 20 + 52 = .
ответ: 136.
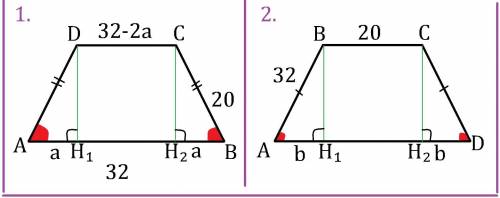
Радиус описанной окружности равностороннего треугольника R=a/√3 (где а-сторона треугольника)
Радиус вписанной окружности равностороннего треугольника r=a/2√3 .
Т.е. R/r=2. А так как площадь круга имеет квадратичную зависимость от радиуса окружности, то и площадь вписанной окружности будет в 2²=4 раз меньше, чем площадь описанной.
Найдем R из длины описанной окружности: R=24π/2π=12 (см)
Найдем площадь описанной окружности:
S₀=πR²=144π, значит площадь вписанной окружности
S₁=144π/4=36π.
Площадь кольца равна разности площадей описанной и вписанной окружностей:
S₀₋₁=S₀-S₁=(144-36)π=108π см²
ответ: площадь кольца 108π см²