Объяснение:
№3
r=S/p (S-площадь p-полупериметр)
p=1/2(AB+AC+BC)=1/2(25+7+24)=28
S=1/2*AC*BC=1/2*7*24=84
r=84/28=3
ответ: 3
№4
Найдем сторону AB по теореме синусов:
AB/ sin90=AC/sin30
AB/1=10/0.5
AB=20
AO=OB (так как радиусы окружности), поэтому
AO=1/2AB=1/2*20=10
ответ: 10
№6
Проведем в треугольнике АВС высоту ВВ1, треугольник АВВ1- прямоугольный
АВ1=АО=7(радиусы окружности)
Треугольник АВС равнобедренный, значит ВВ1 это и биссектриса угла АВС
Рассмотрим треугольник АВВ1:
Найдем сторону АВ по теореме синусов:
АВ/sin 90= AC/sin 60
AB/1=7/ (корень из 3)/2
АВ=(14 корней из трех)/2
ответ: (14 корней из трех)/2
Правильная треугольная призма.
АА1 = 12 см
АВ = 10 см
Найти:S полной поверхности - ?
Решение:Так как данная призма - треугольная, правильная => основание данной призмы - равносторонний треугольник.
Равносторонний треугольник - треугольник, у которой все стороны и углы равны.
=> АВ = ВС = АС = 10 см
S боковой поверхности = Рh, где Р - периметр основания; h - высота призмы.
Р = AB + BC + AC = 3 * 10 = 30 см
h = AA1 = 12 см.
S боковой поверхности = 30 * 12 = 360 см²
S равностороннего △ = а√3/4, где а - сторона треугольника.
S равностороннего △ = 10√3/4 = 5√3/2 см²
S полной поверхности = S боковой поверхности + 2S основания = 360 + (2 * 5√3/2) = 5(72 + √3) см²
ответ: 5(72 + √3) см²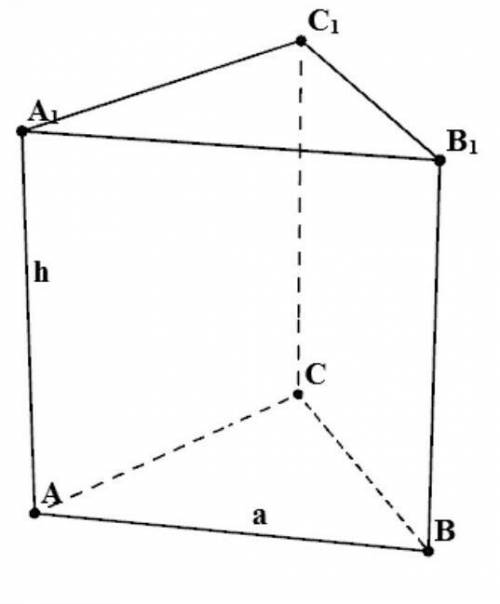
В условии не сказано тангенс какого угла равен √51/7. Рассмотрим оба варианта.
Так как тангенс - это отношение двух катетов, то можно записать:
√51*x - первый катет
7x - второй катет
Найдем гипотенузу по формуле Пифагора:
√(51x²+49x²)=√100x²=10x
1) если tg(a)=√51/7, то
sinb=7x/10x=0,7
2) если tg(b)=√51/7, то
sinb=√51*x/10x=0,1√51