Основания равнобокой трапеции равны 8 см и 18 см. Точка удалена от каждой стороны трапеции на 10 см. Найдите расстояние от этой точки до плоскости трапеции.
———————
ответ: 8 см.
Объяснение:
Назовем данную точку Е.
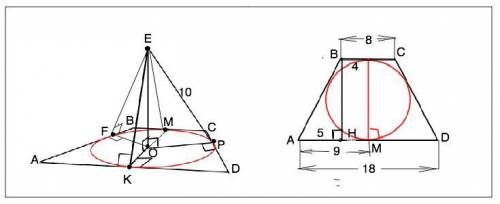
Точка удалена от каждой стороны трапеции на равное расстояние, т.е. на длину перпендикуляров, проведенных от этой точки к сторонам трапеции (см. рисунок во вложении.)
ЕК=ЕF=EM=EP.
Искомое расстояние - перпендикуляр ЕО к плоскости трапеции. Прямоугольные треугольники ЕOF=EOM=EОP=EOK, проекции их гипотенуз - по т. о 3-х перпендикулярах - перпендикулярны сторонам трапеции и равны радиусу вписанной в трапецию окружности.
Суммы противоположных сторон четырехугольника, в который вписана окружность, равны. ⇒ АВ+СD=BC+AD=8+18=26. Боковые стороны равны между собой (дано), ⇒ их длина 26:2=13 см.
Из вершины В трапеции опустим перпендикуляр ВН на АD. Он является высотой трапеции и равен диаметру вписанной окружности.
АН - полуразность оснований. АН=(АD-ВС):2=5.
Из ∆ АВН по т.Пифагора ВН=√(AB²-AH²)=√(13²-5²)=12 см ⇒ d= МК=12, ОК=r=12:2=6 см.
Из ∆ ЕОК по т.Пифагора ЕО=√(EK²-КО²)=√(10²-6²)=8 (см).
1- (Б)
2- (В)
3 - (Г)
4- (Б)
Объяснение:
1) Площа квадрата = а * а
Якщо а=6; 6*6=36 (Б)
2) Діагональ квадрата d=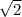 * а ; 8=
* а ; 8= 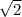 * а ; а= 8 /
* а ; а= 8 / 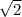 ; тобто сторона квадрата дорівнює 8 /
; тобто сторона квадрата дорівнює 8 / 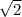 ; а площа звичайно сторону помножити на сторону ( 8 /
; а площа звичайно сторону помножити на сторону ( 8 / 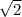 ) * ( 8 /
) * ( 8 / 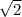 ) = 64/2 (верх множимо на верх а низ множимо на низ).
) = 64/2 (верх множимо на верх а низ множимо на низ).
Дорівнює 32 (тобто В)
3) площа прямокутника це сторона помножена на іншу сторону
6 * 4 = 24
Відповідь - Г
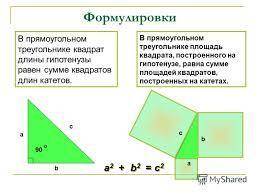
4) Нам потрібно узнати невідому сторону.. по закону АРХІМЕДА ( квадрат діагоналі дорівнює сумі квадратів сторін)
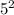 =
=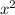 +
+ 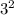 ;
; 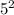 -
- 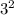 =
= 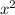 ;
; 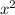 =
= 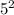 -
- 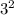 ; х =
; х =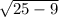 ; х=
; х= 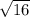 ; х=4
; х=4
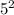 =
=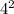 +
+ 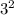
Тобто сторони у нас = 3, та 4. А діагональ між ними = 5
Площа дорівнює 3 * 4 = 12
Відповідь - Б
Составляем пропорцию подобия: BD1/BD=D1E1/DE=18/12=54/DE
DE=54*12/18=36