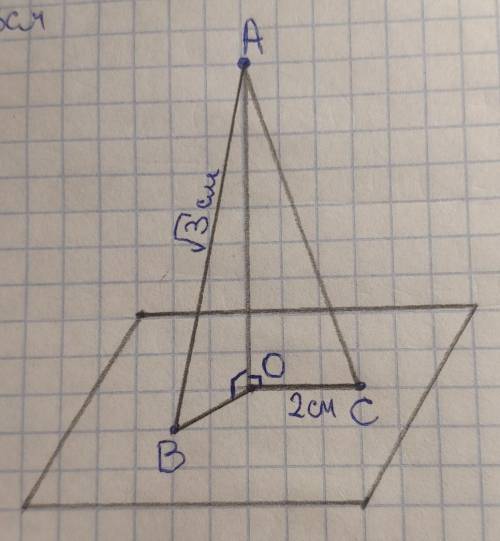
Прямая, перпендикулярная плоскости, перпендикулярна всем прямым, лежащим на этой плоскости.
Следовательно угол АОВ=угол АОС=90°, значит ∆АОВ и ∆АОС – прямоугольные.
ВО+АС=3 см по условию. Пусть ВО=х, тогда АС=3–х.
В прямоугольном ∆АОВ по теореме Пифагора:
АВ²=АО²+ВО²
(√3)²=АО²+х²
АО²=3–х² (Ур 1)
По теореме Пифагора в прямоугольном ∆АОС:
АС²=ОС²+АО²
(3–х)²=2²+АО²
АО²=9–6х+х²–4
АО²=х²–6х+5 (Ур 2)
Подставим значение АО² из уравнения 1 в уравнение 2, получим:
3–х²=х²–6х+5
2х²–6х+2=0
х²–3х+1=0
Д=(–3)²–4*1*1=9–4=5
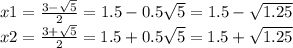
Тогда ВО=1,5+√1,25 или ВО=1,5–√1,25
Катет прямоугольного треугольника всегда меньше гипотенузы, то есть ВО<АВ
1,5+√1,25<√3
1,5+1,118<1,732
2,618<1,732
Неверно
1,5–√1,25<√3
1,5–1,118<1,732
0,382<1,732
Верно, следовательно ВО=1,5–√1,25 см.
Тогда АС=3–(1,5–√1,25)=3–1,5+√1,25=1,5+√1,25
ответ: ВО=1,5–√1,25 см, АС=1,5+√1,25 см.
ответ:
объяснение:
1. рассмотрим параллелограмм авсд.
s=ah, а= 6 это следует h=4
2.рассмотрим δ аве, в=5, h=4. тогда по теореме пифагора
хво2степени =5 в степени2 - 4 в степени2 =9
х=3, т.е. ае=дк=3, это следует
3. ед=ад-ае=3
4. рассмотрим δвед, по теореме пифагора следует
хво 2 степени=3во 2степени+4во второй степени=25
×=5,т.е. вд=5
5.проведем дополнительную высоту ск с вершины с и соединяем с основанием ад
6. рассмотрим δ аск, ак=9, ск=4⇒ по теореме пифагора
хво 2степени=9во2степени+4 во 2степени=97
×=√97, т.е. ас=√97