Объяснение:
Проведем радиус из точки О к точке Е. таким образом АЕ перпендикулярно АВ (касательная). Рассмотрим АЕОД. АДО=АЕО=90, значит два остальных угла также по 90, АЕОД - прямоугольник. АД=ЕО=ОД(радиусы)=АЕ, АЕОД - квадрат. аналогично доказываем с ЕОСВ. Таким образом, получаем равенство сторон АД=ДО=ОС=ВС=ЕВ=ОЕ=АЕ
треугольник АЕО - равнобедренный (АЕ=ЕО) и прямоугольный. а значит углы при основании равны и каждый из них равен (180-90)/2=45, т.е. ЕАО=АОЕ=45.
Аналогично доказываем по треугольнику ОЕВ. ЕОВ=ЕВО=45.
АОВ это сумма двух углов, АОВ=АОЕ+ЕОВ. АОВ=45+45=90, что и требовалось доказать.

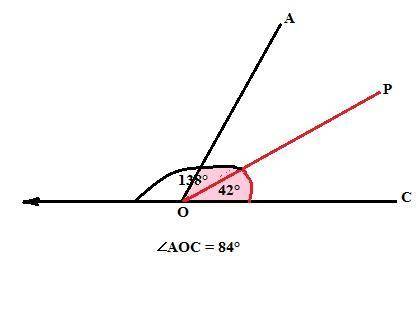
∠АОС = 84°
Объяснение:
Определения:
1. "Дополнительными называются различные лучи, лежащие на одной прямой и имеющие общую граничную точку".
2. "Угол, стороны которого составляют прямую - развернутый угол".
3. "Любой луч, проведенный из вершины развернутого угла, делит его на два угла. Полученные в результате углы имеют одну общую сторону, а две другие составляют прямую. Такие углы называются смежными".
Развернутый угол равен 180°. Угол между биссектрисой ОР угла АОС и лучем, дополнительным к стороне ОС и угол между этой биссектрисой и стороной ОС - смежные углы.
Значит ∠РОС = 180° - 138° = 42°.
∠РОС = ∠АОС : 2, так как ОР - биссектриса.
∠АОС = 2·∠РОС = 2·42 = 84°.
- ВМ=ВК по условию;
- ВР - общая сторона;
- углы МВР и КВР равны, т.к. в равнобедренном треуг-ке АВС высота, проведенная к основанию, является также биссектрисой.
У равных треугольников соответственные углы ВМР и ВКР равны.
б) Треугольники МРО и КРО также равны по двум сторонам и углу между ними:
- МР=КР, т.к. треуг-ки ВМР и ВКР равны (как было доказано выше);
- ОР - общая сторона;
- углы ВРМ и ВРК равны как соответственные у равных треуг-ов ВМР и ВКР.
У равных треугольников МРО и КРО равны соответственные углы КМР и МКР.