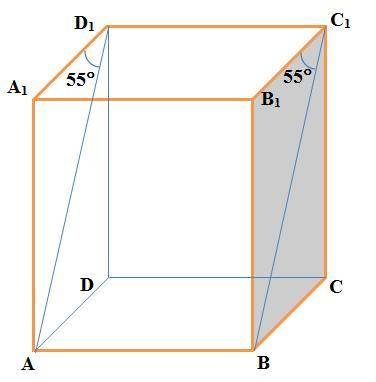
Угол между прямыми C₁B и AA₁ равен 35°
Объяснение:
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
В задаче C₁B и AA₁ являются скрещивающимися прямыми (см. рисунок). Углом между двумя скрещивающимися прямыми называют угол между двумя пересекающимися прямыми, соответственно, параллельными данным скрещивающимся прямым.
В силу этого, так как C₁B || D₁A, то угол между прямыми C₁B и AA₁ равен углу между прямыми D₁A и AA₁, то есть ∠A₁AD₁. В треугольнике ΔAA₁D₁:
∠AD₁A₁+∠D₁A₁A+∠A₁AD₁=180°.
Тогда, так как ∠AA₁D₁=90° и ∠AD₁A₁=55°, то ∠A₁AD₁=180°–90°–55°=35°.
АВ(9;-2);BC(-7;-7);AC(2;-9)
1)расстояние от В доА=|AB|=√9²+(-2)²=√(81+4=√85=9.21;
|BC|=√7²+7²=7√2; |AC|=√4+81=√85=9.21.
2)Xm=Xb+(-7/2)=7-3.5=3.5;Ym=Yb+(-7/2)=1-3.5=-2.5
M(3.5;-2.5);
векторAM(3.5+2;-2.5-3);⇒векторAM(5.5;-5.5);
|AM|=√5.5²+5.5²=5.5√2;
3)длины векторов |AB|=|AC|⇒треугольник равнобедренный;