Для любой правильной призмы справедливы формулы:
Площадь боковой поверхности:
Sбок = Pосн · h, где
Росн - периметр основания,
h - высота.
Площадь полной поверхности:
Sполн = Sбок + 2Sосн
Объем:
V = Sосн · h
____________________
a - сторона основания.
____________________
Правильная треугольная призма:
в основании лежит правильный треугольник, значит
Sосн = 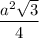
Sбок = 3а · h
Sполн = 3a · h + 2 · a²√3/4 = 3ah + a²√3/2
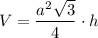
____________________
Правильная четырехугольная призма:
в основании - квадрат, значит
Sосн = a²
Sбок = 4ah
Sполн = 4ah + 2a²
V = a²h
____________________
Правильная шестиугольная призма:
Sосн = 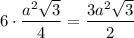
Sбок = 6ah
Sполн = 6ah + 2 · 3a²√3/2 = 6ah + 3a²√3
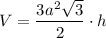
Дано:
АВС - прямоугольный треугольник.
угол А = 90*
Перим. АВС= 14см
R(радиус)=3см
найти:
S (авс) - ?
О - середина ВС. => ОС=R
R= c/2; R= BC/2 => BC= 2R ; BC=6см.
Проведем высоту АО . (из вершины А на ВС).
Докажем, что треуг. АОВ = треуг. АОС
1) АО-общая.
2) ВО=ОС (т.к О - середина ВС)
3) угол ВОА = углу АОС=90* (т.к. АО -высота)
Значит треуг.АОВ=треуг.АОС
След-но АВ=АС(как соответственные элементы) => АВ=4см и АС=4см
S= 1/2 а*в ( * - умножить)
S= 1/2 4*4 = 8см
усе:)